- #36
phyti
- 452
- 8
Windows said:Hello!
Are the transformations such as time dilation, length contraction and relativistic mass just observed ones or real ones?
Thank you.
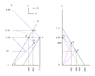
The left drawing shows S' moving at .6c with a .5 unit stick contracted to .4 unit, as measured by S. Three photon events occur, Emission, Reflection, and Detection.
S records (x, t) for E as (0,0), calculates* (x, t) for R as (1.0, 1.0), and for D as
(.75, 1.25).
Due to time dilation, S' records (x', t') for E as (0,0), and for D as (0, 1.00), and calculates* (x', t') for R as (.50, .50).
The right drawing shows events from the S' perspective.
At D, S' expects the S distance to be .60 according to his clock, placing him at D'. Since the S distance is .75, he concludes the S frame moving at -.6c is contracted by .80.
The perception of a length contracted S frame is a reciprocal effect of time dilation for S'.
The motion induced effects on the S' frame are real in the sense of being independent of observation. The S' observation of the world beyond his frame is conditioned by those same effects, resulting in an altered perception, that does not correspond to reality outside the mind.
*Dividing the round trip time in half per SR definition of simultaneity.