Explore Space-Proper-Time Diagrams - Where's the Catch?

[Jorrie]

Here's something that puzzled me for some time: why are space-proper-time (SPT) diagrams not used more frequently? I did search this forum for the term, but without success. It may be known under some other technical term that I don't know about.

I'm using the term with the meaning as per Lewis Carroll Epstein's "Relativity Visualized", where the orthogonal axes of two inertial coordinate systems in relative motion are simply rotated by an angle phi = asin(-v/c) relative to each other, as shown in the attached figure for a relative velocity (red coordinates relative to blue coordinates) of v = 0.8c.

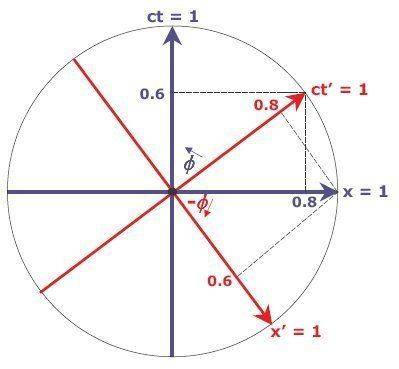
I originally thought that SPT diagrams represent a weird combination (as Kip Thorne wrote) of "my space and your time" but the more I toyed with SPTs, the more useful they seemed. I think one problem is that SPT diagrams cannot show space-like intervals, but for time-like intervals, they seem to be much easier to picture and use than Minkowski space-time diagrams.

For one thing, the calibrating marks on the two sets of orthogonal axes have identical lengths. Other benefits that I can think of include:
i) Time dilation and Lorentz contraction are both read off directly by projecting one coordinate system's proper-time intervals or space intervals onto the other system.
ii) It shows the freedom of choice of reference system very clearly - no preferred frame is remotely suggested - just rotate the chart!
iii) A straight vector summation of a space interval and a proper-time interval gives a "space-proper-time interval" that is invariant under change of inertial frames. There may be an official term for this interval, but I don't know it.
iv) Maybe more…

Apart from space-like intervals, I still have to find a situation that cannot be represented on the SPT diagram. I know that here velocity additions cannot be done by adding angles as in the rapidity case, but still…

So where's the catch? I fully expect to be hand-slapped for suggesting that SPT diagrams could be useful, but I simply must know "if not, why not?"

Jorrie

 

[Chris Hillman]

Well, have you thought about light cones? Unless your diagrams fully capture the causal properties in relativistic kinematics, as does Minkowski's geometry, they are probably of limited utility. And have you thought about how your diagrams at the level of tangent spaces on a Lorentzian manifold would relate to the causal structure of the manifold? (Compare the "absolute future" of an event in a Lorentzian manifold.) You also said something about "tick marks" which sounds to me like some kind of misconception.

Just off the top of my head...

 

[Jorrie]

Thought about some!

Hi again Chris and thanks for commenting!

Well, have you thought about light cones? Unless your diagrams fully capture the causal properties in relativistic kinematics, as does Minkowski's geometry, they are probably of limited utility.

Yep, it seems to me that the cones are opened up into two touching semi-spheres. Everything on the positive time side represents the future light cone of Minkowski and the opposite side represents the past light cone. All points inside the light cones are represented and nothing else.

... And have you thought about how your diagrams at the level of tangent spaces on a Lorentzian manifold would relate to the causal structure of the manifold? (Compare the "absolute future" of an event in a Lorentzian manifold.)

I must think about this one - however the top semi-sphere represents the absolute future of an event at the origin and the bottom semi-sphere the absolute past.

... You also said something about "tick marks" which sounds to me like some kind of misconception.

I wrote "… the calibrating marks on the two sets of orthogonal axes have identical lengths.", which simply means that the scale of the axis for both systems are identical - unlike a Minkowski diagram's scale that is different for systems in relative motion. By 'scale' I mean the physical distance on the chart that represents a unit of space or time.

I find a layperson to grasp things much faster on these space-proper-time diagrams, but then, I'm a little worried about side-effects…

Regards, Jorrie

 

[Mortimer]

This picture

illustrates how your proper-time-space diagram relates to the lightcone and Minkowski diagrams. It also shows where the space-like intervals have gone. Note that the cone in the picture is not the lightcone.
(from Hans Montanus: Proper Time Physics, Hadronic Journal 22, 625-673, 1999)

 

[Chris Hillman]

I wrote "… the calibrating marks on the two sets of orthogonal axes have identical lengths.", which simply means that the scale of the axis for both systems are identical - unlike a Minkowski diagram's scale that is different for systems in relative motion. By 'scale' I mean the physical distance on the chart that represents a unit of space or time.

This is what I was squawking about before--- you are insisting that "physical distance" can only mean euclidean distance. That is likely to get you into awful trouble when you try to read the literature.

BTW, that's another reason to be careful about using these diagrams unless you are know exactly how to relate them to standard techniques--- the literature uses Minkowski geometry visualized as, well, Minkowski geometry! So using these diagrams may well be more trouble than they are worth, particularly since the benefits (if any) seem unclear.

 

[Jorrie]

This picture ... illustrates how your proper-time-space diagram relates to the lightcone and Minkowski diagrams. It also shows where the space-like intervals have gone. Note that the cone in the picture is not the lightcone.

Hi Mortimer,

I'm afraid I do not understand the relationships (I must say the diagrams come out a bit tiny on my computer). If you can, give a bit more info. Otherwise I will try to locate the document that you referenced.

Jorrie

 

[Jorrie]

The squakes and the squeeks

Hi Chris, you wrote:

This is what I was squawking about before--- you are insisting that "physical distance" can only mean Euclidean distance.

No, no! You read more into what I said than what I said - sigh - words without diagrams or math are so damn vague --- but this one can be in words! The "physical distance" I mentioned is what I measure on a piece of good old graph paper (never on a computer screen, I decided in my days of Varian mini-computers…)

The moving frame sports, on the graph paper, stretched Minkowski "physical distances" according to my desk ruler --- yet I tell people that it represents Lorentz contraction. I know the reasoning and I agree that it is correct, but try telling that to a bunch of engineers with only a passing interest in relativity!

I agree with you about the difficulty in converting the SPT representation to the standard literature and as such, I do not use it. However, I do toy with the idea from time to time...

Regards, Jorrie

 

[Mortimer]

Hi Mortimer,

I'm afraid I do not understand the relationships (I must say the diagrams come out a bit tiny on my computer). If you can, give a bit more info. Otherwise I will try to locate the document that you referenced.

Jorrie

For a chosen x-axis in the Minkoswki diagram, the $c \tau$-axis is added perpendicular to the x-ct plane, kind of as a 5th dimension. A worldline in the Minkowski plane can now be projected in the direction of the $c \tau$-axis to the cone in the picture. From the projection, one can directly read the $c \tau$ value. The relation is the classic one: $(c \tau)^2=(ct)^2-x^2-y^2-z^2$. An acceleration, which shows in the Minkowski diagram as change in inclination of the worldline, will show in the x-$c \tau$ plane as a rotation along the edge of the cone.

The articles of Montanus are a bit hard to come by. You can find a scanned copy of the referenced article http://home.hetnet.nl/~f2hrfjvanlinden171/Montanus-ProperTimePhysics.pdf" (11MB !).

 

[Jorrie]

Oh no! Absolute Frame?

Thanks Mortimer, I downloaded the article:

The articles of Montanus are a bit hard to come by. You can find a scanned copy of the referenced article http://www.euclideanrelativity.com/Montanus-ProperTimePhysics.pdf" (11MB !).

I read the first half and am very disappointed to see that it is "absolute Euclidean spacetime" with a preferred universal frame of reference! The premise that clocks stationary in this frame are the "fastest" and that all clocks moving relative to this frame "run slower" is obviously nonsense. If it was so, it would be very simple to detect...

BTW, the space-proper-time (SPT) diagrams that I'm talking about says nothing of that sort. It is relative spacetime and is fully Minkowski compatible for time-like and light-like intervals. I find SPT diagrams in many cases easier to use, but they represent nothing new!

Regards, Jorrie

 

[Mortimer]

I agree with you. I do not support absolute euclidean space-time either. It is not a requirement anyway. The diagrams are very usable and can equally well be applied in relative space-time. I just wanted to show the relation between the SPT and Minkowski diagrams.

 

[robphy]

I find a layperson to grasp things much faster on these space-proper-time diagrams, but then, I'm a little worried about side-effects…

Regards, Jorrie

I'm not 100% sure... but your diagrams might be more commonly known as Loedel or Brehme diagrams. Of course, Minkowski diagrams and its associated geometry appeared first [almost a hundred years ago].

So what specific "things" do you find that "the layperson grasps [] much faster on these space-proper-time diagrams"? It may be that the presentation of that "thing" for the Minkowski diagram is inadequate. Please specify these "things".

It might be a valuable exercise [and maybe a worthy contribution to the literature] to fully compare these alternative diagrams with the Minkowski diagrams.
By fully compare, I mean: for each diagram,

• represent inertial observers (and uniformly accelerated observers)
• represent light rays
• represent spatial displacements
• represent spacetime intervals and discuss causal structure
• display the "clock ticks" along the inertial worldlines
• construct the diagram from another inertial observer's frame
• represent the vector-space properties found in Minkowski space
  • how do you scalar-multiply a displacement?
  • how do you add two displacements [of possibly different types (e.g., timelike+lightlike)]?
  • how do you represent an inertial observer's "space" (i.e., the subspace Minkowski-orthogonal to an inertial observer's worldline)?
• do explicit examples of the various "effects" (time-dilation, length-contraction, doppler effect, velocity composition, headlight effect, particle dynamics) and operational measurements (radar, Bondi k-calculus)
• display the 2+1 and 3+1 (rather than merely 1+1) cases
• represent the nonrelativistic limit
• how would spacetime curvature be represented? and how would the diagram be the limit of zero-curvature?

At some point, I may take up such a study... to at least settle for myself the strength of the Minkowski approach.

 

[Jorrie]

I'm not 100% sure... but your diagrams might be more commonly known as Loedel or Brehme diagrams...

Thanks robphy, I found one article on a simplified Brehme diagram, with an annex that showed the complete Brehme diagram: http://www.colvir.net/prof/richard.beauchamp/rel-an/rela.htm".

This is exactly what I had in mind, except that I labeled my axes differently (and wrongly, I think!) It looks like the x' and ct orthogonal axes go together and then the orthogonal x and ct' axes. Makes somewhat sense. It is a space-propertime diagram, after all!

So what specific "things" do you find that "the layperson grasps [] much faster on these space-proper-time diagrams"? It may be that the presentation of that "thing" for the Minkowski diagram is inadequate. Please specify these "things".

It might be a valuable exercise [and maybe a worthy contribution to the literature] to fully compare these alternative diagrams with the Minkowski diagrams.

Yes, I think this will not be too difficult! I will start on such a comparison and see how far I get.

Thanks again and regards,

Jorrie

 

[Chris Hillman]

Hi all,

I wrote:

This is what I was squawking about before--- you are insisting that "physical distance" can only mean euclidean distance. That is likely to get you into awful trouble when you try to read the literature.

Jorrie protested:

No, no! You read more into what I said than what I said - sigh - words without diagrams or math are so damn vague --- but this one can be in words! The "physical distance" I mentioned is what I measure on a piece of good old graph paper (never on a computer screen, I decided in my days of Varian mini-computers…)

Jorrie, I know that's what you meant, and that's exactly why I protested. In principle I should explain, but the topic is insufficiently important, and in any case I am too disheartened by the turn this thread has taken:

(from Hans Montanus: Proper Time Physics, Hadronic Journal 22, 625-673, 1999)

I read the first half and am very disappointed to see that it is "absolute Euclidean spacetime" with a preferred universal frame of reference! The premise that clocks stationary in this frame are the "fastest" and that all clocks moving relative to this frame "run slower" is obviously nonsense. If it was so, it would be very simple to detect...

It is my own rule to leave a thread as soon as "Hadronic Journal" or another fringe topics which I have tried to address in some previous instar is mentioned; it's never worth the hassle.

 

[Jorrie]

Don't worry!

...
It is my own rule to leave a thread as soon as "Hadronic Journal" or another fringe topics which I have tried to address in some previous instar is mentioned; it's never worth the hassle.

Hi Chris, we agree and have left the "Hadronic Journal", so be patient... We have not established (yet) that "space-propertime diagrams" or Brehme diagrams are quite fringe topics! As Robphy has suggested, maybe we can put them to bed properly or 'rediscover' something useful...

Regards, Jorrie

 

[Jorrie]

What diagram?

I agree with you. I do not support absolute euclidean space-time either. It is not a requirement anyway. The diagrams are very usable and can equally well be applied in relative space-time. I just wanted to show the relation between the SPT and Minkowski diagrams.

Hi Mortimer,

I'm not quite sure that the SPT diagram is equivalent to the diagrams that you referenced. There seems to be something 'funny' with the 'Montanus diagram'. I think the Brehme diagram is a much more natural variant of the Minkowski spacetime diagram, which do not invite 'alternate physics'.

In any case, one would only know if some reasonably comprehensive list of scenarios are compared for different diagrams, as suggested by robphy. The question is: is it worth the effort?

Jorrie

 

[Ich]

Just try to add a third coordinate system to a Minkowski diagram and to a Loedel diagram. That´s the catch.

 

[Jorrie]

Loedel vs SPT diagram

Hi Ich, thanks for your input:

Just try to add a third coordinate system to a Minkowski diagram and to a Loedel diagram. That´s the catch.

Agreed for the Loedel/Brehme diagrams with their oblique reference frame axes. The space-propertime (SPT) diagram has regular orthogonal axes and IMO it does not suffer from this "catch".

However, the SPT diagram may have other catches, apart from the fact that it's a 'non-standard' representation.

Jorrie

 

[Ich]

Agreed for the Loedel/Brehme diagrams with their oblique reference frame axes. The space-propertime (SPT) diagram has regular orthogonal axes and IMO it does not suffer from this "catch".

I must have missed something. What exactly is the difference between a Loedel diagram and a SPT? Is the diagram you posted initially labeled correctly?

 

[Jorrie]

Gone with SPT!

I must have missed something. What exactly is the difference between a Loedel diagram and a SPT? Is the diagram you posted initially labeled correctly?

Yep, it was labelled correctly as far as SPT diagrams go... i.e., orthogonal axes pairs (rotated) and not an oblique reference time axis like Loedel/Brehme.

But, I can now see that, without awkward manipulation, such a scheme (SPT) cannot give you the Lorentz transformation of space- and time intervals between two inertial frames in relative motion. So that is the SPT catch, a fatal one, I think!

Jorrie

 

[Ich]

Ah, I see. Maybe a slightly modified SPT diagram could be useful to explain ordinary rotations to your engineers?