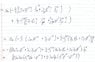Deriving Field Equations for Real Vector Fields using Euler-Lagrange (Tensors)

[ballzac]

Homework Statement

Show that the Lagrangian density:
$$L=- 1/2 [\partial_\alpha \phi_\beta ][\partial^\alpha \phi^\beta ]+1/2 [\partial_\alpha \phi^\alpha ][\partial_\beta \phi^\beta ]+1/2 \mu^2 \phi_\alpha \phi^\alpha$$
for the real vector field $$\phi^\alpha (x)$$ leads to the field equations:

$$[g_\alpha\beta (\square +\mu^2)-\partial_\alpha \partial_\beta]\phi^\beta=0$$

Homework Equations

$$\partial L/\partial\phi-\partial_\alpha (\partial L/\partial\phi_{,\alpha})=0$$

The Attempt at a Solution

We've only just started learning a little bit about tensors, and I am finding questions like this quite difficult. In the lectures we have not covered cases when the field is also a tensor. I know about raising and lowering indices using the metric tensor, and combining ∂s with kronecker delta. Here is what I have tried so far. I have changed some of the indices to avoid problems (Did this need to be done?)...

I've also done a bit that I typed up a while ago, but I started changing some of it and now that I look at it, it doesn't really make any sense, but I think I have the first term of the Euler-Lagrange equation working. I'm not sure if it's quite right, but it begins and ends with the right expression, so it's at least partly right. However, the bit in the image I've uploaded does not lead me to the right answer, so this is where I really need help. Hopefully someone can give me some pointers. Thanks :)

 

[samr]

Ok first post on here so sorry if I screw up the formatting :)

So anyways, starting with the individual terms of the E-L:
$$\frac{\partial\mathcal{L}}{\partial\phi}=\mu^2\phi_\alpha=g_{\alpha\beta}\mu^2\phi^\beta$$
And the second term:
$$\frac{\partial\mathcal{L}}{\partial\left(\partial_\alpha\phi\right)}=-\partial_\alpha\phi_\beta + \partial_\beta\phi^\beta$$
Which then gives us:
$$\partial_\alpha\left(\frac{\partial\mathcal{L}}{\partial\left(\partial_\alpha\phi\right)}\right)=-\partial_\alpha\partial_\alpha\phi_\beta + \partial_\alpha\partial_\beta\phi^\beta=-g_{\alpha\beta}\square\phi^\beta +\partial_\alpha\partial_\beta\phi^\beta$$

Finally the two of these leave us with the desired equation.

 

[ballzac]

You can preview you post, but I don't think you can do it in the quick reply thing. You need to click "New Reply" or "go advanced"

If you're wondering why your tex isn't working, the last tag needs a forward slash thus: /tex

Looking forward to your input. :)

 

[samr]

Balllzac - yeah I was just checking on a few things.

My indices may be a bit confused - as it's still early morning for me and I don't have my head in it. I'll give this a reread in about ten minutes and do corrections.

And yeah I think I've messed up the indices on the LHS of the final equation. Tried to make too many jumps ahead in one go.

 

[ballzac]

So clearly I was wasting my time introducing deltas. Is there also no need to change indices? In one of the worked examples from the lecture notes "dummy indices" are introduced. Although I sort of follow what you've done for the first term (which is pretty much how I did it), I'm not sure I fully understand the rules. Obviously it is equivalent to
$$d/dx 1/2 x^2 = x$$
but, for instance, is there a particular reason that you end up with a covariant index rather than contravariant? These are the sorts of things that I'm having trouble with, particularly since in the lectures there was no mention of greek indices on the field.

The second term is confusing me. Is there an extra step after the first = that would help explain how you got that? (oh, I just read the edited version of you post, so my last comment becomes kind of superfluous.)

Thanks for all the help Samr :)

 

[samr]

Yeah I missed out on the steps inbetween the second E-L term and what it equals in your example Lagrangian density. I'll fill in these gaps later today if that's okay with you :)

 

[Hao]

Whether you end up with a contravariant or covariant index can be a matter of convention, depending on which version of the Euler-Lagrange equation you pick.

For example, both
$$\frac{\partial L}{\partial \phi^i} = \partial^j \frac{\partial L}{\partial \phi^{i,j}}$$
$$\frac{\partial L}{\partial \phi_i} = \partial_j \frac{\partial L}{\partial \phi_{i,j}}$$
are equally valid.

 

[ballzac]

Yeah I missed out on the steps inbetween the second E-L term and what it equals in your example Lagrangian density. I'll fill in these gaps later today if that's okay with you :)

I'm sure I can handle that, lol. Thanks for going to the effort.

Whether you end up with a contravariant or covariant index can be a matter of convention, depending on which version of the Euler-Lagrange equation you pick.

For example, both
$$\frac{\partial L}{\partial \phi^i} = \partial^j \frac{\partial L}{\partial \phi^{i,j}}$$
$$\frac{\partial L}{\partial \phi_i} = \partial_j \frac{\partial L}{\partial \phi_{i,j}}$$
are equally valid.

Aaah, that makes sense. I hadn't seen the Euler-Lagrange equation written with indices on phi. Thanks.

PS: Samr, I'm more interested in understanding how to solve these than just knowing the answer, so feel free to just briefly explain rather than type out a solution if it is easier for you. Thanks again.

 

[samr]

Ok well I'll try to explain each term individually then :) (this is a nice break from work)

https://www.physicsforums.com/latex_images/22/2218689-0.png

[/URL]
Well this is by far the simplest term as we know that the final (potential) term in the lagrangian density $\frac{1}{2}\mu^2\phi^\alpha\phi_\alpha$ is a tensor product $\phi_0^2\pm\phi_i^2$ (with the sign being dependant on the convention of the minkowski metric $diag(+---)$ or $diag(-+++)$).
So this is effectively a quadratic term in $\phi^2$ as such differentiates normally. Where in my answer I inserted the metric to change the contra to covariant $\phi_\beta$ as this is the form given in the question's answer.

For the second term things are a little more difficult to see right away, and generally the best thing to do is just practice until you feel happy about how things like this differentiate.

https://www.physicsforums.com/latex_images/22/2218689-1.png

[/URL]
This term comes from $$\mathcal{L}_{\partial\phi}=- 1/2 [\partial_\alpha \phi_\beta ][\partial^\alpha \phi^\beta ]+1/2 [\partial_\alpha \phi^\alpha ][\partial_\beta \phi^\beta ]$$
We can again treat the first of these terms $-1/2[\partial_\alpha \phi_\beta ][\partial^\alpha \phi^\beta]$ as a quadratic from the implied summation, thinking of it something like $\left(\partial\phi\right)^2$, so we end up with $-\partial_\alpha\phi_\beta$ with the contra- or co- variance depending on which convention you're using (see Hao's post). I chose my convention by looking at the "show that" part of the question and seeing this was the most helpful form to have it in (rather than playing about with 2 metric terms going to a delta function).

The final term $\partial_\beta\phi^\beta$ comes from (again) similar arguments, but again notice that we have the summation going between the partial derivative and the field $\phi$, giving us a term looking like $\left(\left(\partial_\tau\phi\right)^2\pm\left(\nabla_a\phi^a\right)^2\right)$ squared, which differentiates to the term I gave.

I guess the thing they're trying to get you to look at with this question is where the summations are. Whether between corresponding terms, or between the partial derivate and the field. i.e. the two different terms we had are not equivalent $\left|\partial_\alpha\phi_\beta\right|^2\neq\left(\partial_\alpha\phi^\alpha\right)^2$

Also of note whichever of the two styles of the E-L you chose from Hao's post - just make sure you're consistent! :)

also your attachment hasn't ever worked for me so I honestly don't know where your mistakes were so all I can do is lead you through my approach, if you need anything else clarifying just ask :)

 

[ballzac]

Wow. Thanks for such a detailed response. I think I will have to meditate on it for a while and absorb it, but I think you've given me the tools I need to understand this. I just realized that my image says "pending approval" which is why you can't see it. I would have just typed it up if I realized it would not show straight away. Anyway, it's clear that I was going about it the wrong way.

No doubt I will have more questions, but for now you have given me a lot to think about. Thank you so much. :D

 

[samr]

No problem at all - it's a particularly awkward topic if you're not completely familiar with tensor algebra and notation, with quite a few minor pitfalls to be had. Saying that, it's one of the most important tools in modern physics (mathematically).

 

[ballzac]

Okay, I'm still having trouble getting this bit...
$$-\partial_\alpha\partial_\alpha\phi_\beta =-g_{\alpha\beta}\square\phi^\beta$$
I don't understand how the indices change. For example, how does the index on phi remain beta, but change from covariant to contravariant?

 

[samr]

Since you're just looking at the term on its own and there is no implied sum it is effectively a dummy variable. $\partial_\alpha\phi^\beta=\partial_\gamma\phi^\rho=\dots$

Ah sorry I misunderstood what you were asking give me a few minutes.

MY LHS is wrong.

 

[ballzac]

hmmm, okay that makes sense. But now that you mention the summation...There is no summation on the left hand side, yes? Because the repeated index is covariant in both occurances. But then on the right hand side there is a summation within the D'alembert operator. This also has me confused.

 

[samr]

Looking at the first term in the lagrangian density - does it help to think about the implied sum between the two partial derivatives, and the fact that since $x_\mu x^\mu=x^\mu x_\mu$ subbing $x_\mu\rightarrow\partial_\mu$? This may help clear the problem up.

In reference to your post my LHS is wrong :) it's my fault for skipping steps.

 

[Hao]

It is worthwhile returning to kronecker deltas and metrics when in doubt. The offending term is
$$L_1 = -\frac{1}{2}\partial_a\phi_b\partial^a\phi^b = -\frac{1}{2}g^{a m}g^{b n}\partial_a\phi_b\partial_m\phi_n$$

In contravariant notation,
$$\frac{\partial L_1}{\partial \phi_{i,j}} = -\frac{1}{2}g^{a m}g^{b n}(\delta^{j}_{a}\delta^{i}_{b}\partial_m\phi_n + \delta^{j}_{m}\delta^{i}_{n}\partial_a\phi_b) = -\frac{1}{2}(\delta^{j}_{a}\delta^{i}_{b}\partial^a\phi^b + \delta^{j}_{m}\delta^{i}_{n}\partial^m\phi^n) = -\frac{1}{2}(\partial^j\phi^i + \partial^j\phi^i) = -\partial^j\phi^i$$
If you recognize that a,b,m,n are all dummy indices, you could skip the second last and third last steps.
$$\partial_j \frac{\partial L_1}{\partial \phi_{i,j}} =-\partial_j\partial^j\phi^ i= -\square^2 \phi^i$$

If we worked in covariant notation,
$$\partial^j \frac{\partial L_1}{\partial \phi^{i,j}} =-\partial^j\partial_j\phi_i = -\square^2 \phi_i = - g_{ia}\square^2\phi^a$$

One quick method to check your answers is by counting indices.
If we treat:
1) a contravariant index as +1
2) a convariant index as -1
3) 1 / (a contravatiant index) as -1
4) 1 / (a covariant index) as +1

Counting indices for the various equations, we have for:
1) L = 0 (as expected because it is a Lorentz invariant.)
2) $$\square^2 \phi^i$$ = 1
3) $$g_{ia}\square^2\phi^a$$ = -2 + 1 = -1
4) $$\frac{\partial L_1}{\partial \phi_{i,j}}$$ = 0 + 2 = 2
5) $$\frac{\partial L_1}{\partial \phi^{i,j}}$$ = 0 - 2 = -2
6) $$\partial_j \frac{\partial L_1}{\partial \phi_{i,j}}$$ = -1 + 2 = 1
7) $$\partial^j \frac{\partial L_1}{\partial \phi^{i,j}}$$ = 1 - 2 = -1

Note that counting for [(2) and (6)], and [(3) and (7)] give the same answer, which is what we would expect for the LHS tensor and RHS tensor to have the same number of contravariant and covariant indices.

We may also note that
$$\partial_i = \frac{\partial}{\partial x^i}$$
$$\frac {\partial x^i}{\partial x^j} = g^{i}_{j} = \delta^{i}_{j}$$ (orthogonal coordinates)

 

[ballzac]

Thanks heaps for that Hao. It's taken me a while to actually follow it, but I think I get it now. I still need a lot of practice before I get how these things work, but you guys have definitely put me on the right track.