- #1
D.S.Beyer
- 50
- 2
My interest surrounds the qualities and affects of gravitational length contraction (GLC).
Like most other General Relativity circumstances GLC is difficult to measure because of frame of reference issues (such that a meter in space is longer than a meter on Earth but in both frames of reference a meter measures a meter).
But what really confounds me are the affects of GLC as it relates to a broader view of spacetime. Below is a question regarding distance:
-
A, B and C are points in 'free space'. B views the distance between A and C to be 1 parsec. A and C both agree that they appear 1 parsec from each other. The 'fence posts' are simply a graphical way of saying that every distance is the same relative to each other.
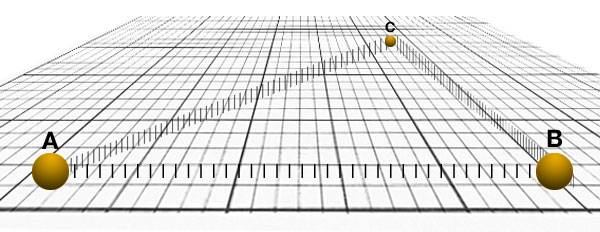
A stray neutron star has moved between A and C. The neutron star has contracted the space around it.
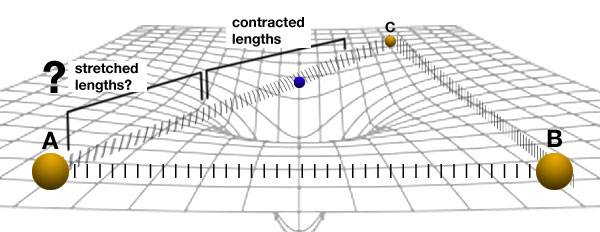
My questions are:
"Does the distance between A and C increase?"
"If the distance does not increase, then, since the lengths around the neutron star are contracted are other distances dilated (stretched) to maintain a constant distance?"
"If the distance does not increase and other space is not dilated, do A and C 'pull' closer to each other, even if they are well outside the neutron stars gravitational influence? And does B view this?"
(Thanks for putting up with my photoshop skills. Slowly I am beginning to understand the bizarre construct of spacetime, in great part due to the physics forums. Thanks everyone!).
Like most other General Relativity circumstances GLC is difficult to measure because of frame of reference issues (such that a meter in space is longer than a meter on Earth but in both frames of reference a meter measures a meter).
But what really confounds me are the affects of GLC as it relates to a broader view of spacetime. Below is a question regarding distance:
-
A, B and C are points in 'free space'. B views the distance between A and C to be 1 parsec. A and C both agree that they appear 1 parsec from each other. The 'fence posts' are simply a graphical way of saying that every distance is the same relative to each other.
A stray neutron star has moved between A and C. The neutron star has contracted the space around it.
My questions are:
"Does the distance between A and C increase?"
"If the distance does not increase, then, since the lengths around the neutron star are contracted are other distances dilated (stretched) to maintain a constant distance?"
"If the distance does not increase and other space is not dilated, do A and C 'pull' closer to each other, even if they are well outside the neutron stars gravitational influence? And does B view this?"
(Thanks for putting up with my photoshop skills. Slowly I am beginning to understand the bizarre construct of spacetime, in great part due to the physics forums. Thanks everyone!).