- #1
Patdon10
- 85
- 0
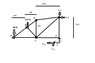
The problem is attached. I have to solve for the force in the member BC. The thing I need help with is solving for the two attachments. I already broke it down into the forces and directions, but what do I do with the lower attachment? How do I find the x displacement of point G from E if I'm trying to find the moment at point E about G. I understand the ratio is supposed to help me, but how? This problem would be much simpler if truss FG wasn't there, and the support was at point F.