- #1
Coin
- 566
- 1
So I was lucky enough to visit CERN earlier this year, and they were selling t-shirts with a long equation on them. And I, like an idiot tourist, somehow jumped to the conclusion this was the standard model Lagrangian and got the t-shirt.
Well, it's still a pretty cool t-shirt, but then I went and looked up the SM lagrangian and it seemed to come in two flavors, one four times this long and one about 50 times this long. Oops...
I lack a particle physics background, so-- I think I know what some of these symbols might mean, but honestly, not most of them! Any help appreciated, what is this equation I am wearing?
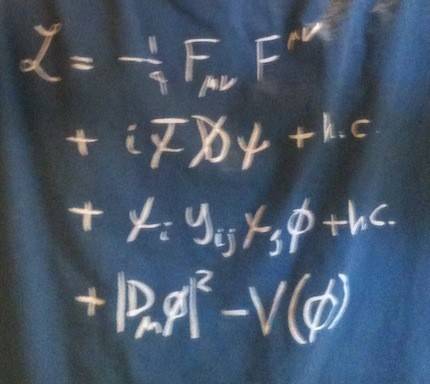
Well, it's still a pretty cool t-shirt, but then I went and looked up the SM lagrangian and it seemed to come in two flavors, one four times this long and one about 50 times this long. Oops...
I lack a particle physics background, so-- I think I know what some of these symbols might mean, but honestly, not most of them! Any help appreciated, what is this equation I am wearing?