- #1
pc2-brazil
- 205
- 3
Homework Statement
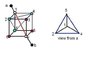
Twelve resistors, each one with a resistance of R ohms, form a cube (see attached figure). Find R17, the equivalent resistance of a diagonal of the cube.
(The first attached picture was scanned from the book "Physics" by Halliday, Resnick and Krane, 4th edition.)
Homework Equations
The Attempt at a Solution
I used the fact that, by symmetry, the potential at points 2 and 4 is equal, and the potentials at points 8 and 6 are equal. So, I redrew the resistor configuration and did some simplifications, as the second attached picture shows.
This symmetry argument worked perfectly to show that the resistance between points 1 and 3 (the equivalent resistance of the diagonal of a face) is 3R/4, but it is not working to show that the resistance between points 1 and 7 is 5R/6 (which is the answer given by the book).
I'm stuck at the last simplification attempt shown in the picture.
Thank you in advance.