- #1
LearninDaMath
- 295
- 0
1. Homework Statement
The derivative of s(t) = (976(.835)^t - 1) +176t
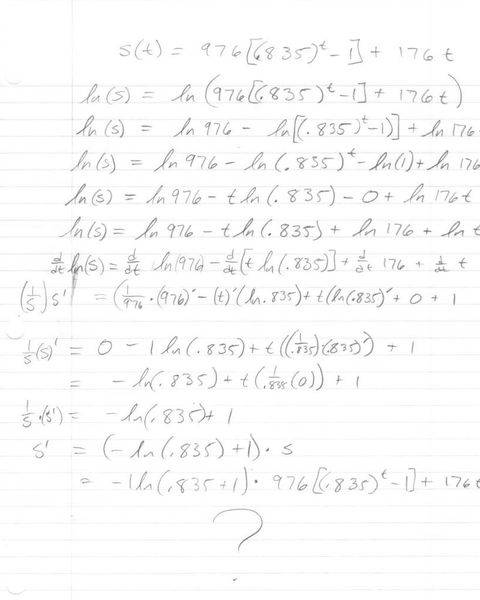
I have to take ln of both sides to bring the t down from the exponent. But I never had to apply ln to an equation of this complexity. Here is my attempt, but it doesn't even look close to being on the correct path...what I'm I doing wrong? I'm guessing I'm messing up a step pretty early on in this problem. Can you locate my confusion? EDIT: the t on the 176t got cut off when scanned, but its supposed to be there on the 3rd and 4th lines..
The derivative of s(t) = (976(.835)^t - 1) +176t
I have to take ln of both sides to bring the t down from the exponent. But I never had to apply ln to an equation of this complexity. Here is my attempt, but it doesn't even look close to being on the correct path...what I'm I doing wrong? I'm guessing I'm messing up a step pretty early on in this problem. Can you locate my confusion? EDIT: the t on the 176t got cut off when scanned, but its supposed to be there on the 3rd and 4th lines..
Last edited: