- #1
PeachBanana
- 191
- 0
Homework Statement
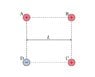
If you calculate W, the amount of work it took to assemble this charge configuration if the point charges were initially infinitely far apart, you will find that the contribution for each charge is proportional to kq^2/L. In the space provided, enter the numeric value that multiplies the above factor, in W.
Homework Equations
Vba = Vb - Va = -Wba / q
The Attempt at a Solution
I need to sum the electric potentials to find the electric potential at one point. The potential due to charge A before "B" is placed there is:
kq / L
The potential due to charge B before "C" is placed is:
where I'm having problems. It states the point charges were initially infinitely far apart so I'm not sure how that affects "L."