- #1
whereisccguys
- 21
- 0
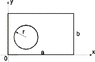
A thin rectangular plate of uniform areal density 2.96 kg/m2 has length 42.0 cm and width 26.0 cm. The lower left hand corner is located at the origin, (x,y)= (0,0) and the length is along the x-axis. There is a circular hole of radius 5.50 cm with center at (x,y)=(15.00,11.00) cm in the plate.
Calculate the distance of the plate's center of mass from the origin.
this was a 2 part questions, first part was find the mass of the plate which i got was .295 kg... the second part is calculate the distance of the plate's center of mass from the origin... my attempt to solve this problem was to divide the plate into three pieces of the x direction and then get each mass, it's distance on X, multiple each piece of mass by it's distance from X and add them up and divide by the total mass of .295 kg... and then i do the same for the Y direction... whcih gives me a center of mass at (.2984, .1756) in meters and finally givin me a distance of .3462 m from the point of origin... but this gives me the wrong answer... anyone knoe what i did wrong and if there is another way to do it?
Calculate the distance of the plate's center of mass from the origin.
this was a 2 part questions, first part was find the mass of the plate which i got was .295 kg... the second part is calculate the distance of the plate's center of mass from the origin... my attempt to solve this problem was to divide the plate into three pieces of the x direction and then get each mass, it's distance on X, multiple each piece of mass by it's distance from X and add them up and divide by the total mass of .295 kg... and then i do the same for the Y direction... whcih gives me a center of mass at (.2984, .1756) in meters and finally givin me a distance of .3462 m from the point of origin... but this gives me the wrong answer... anyone knoe what i did wrong and if there is another way to do it?