- #1
Fantasist
- 177
- 4
I have a classical mechanics problem related to the constrained motion of a mass:
as per the attached graphics, assume a thin rigid rod of length L and mass m moving frictionless constrained to a rail such that is always locally perpendicular to the latter. The rod starts off with speed v=v0 in the straight path of the rail. My question is, what is the speed in the apex of the curved section (half a circle with radius R), and what is the speed after it is in the straight section again? There are no external forces acting.
Thanks.
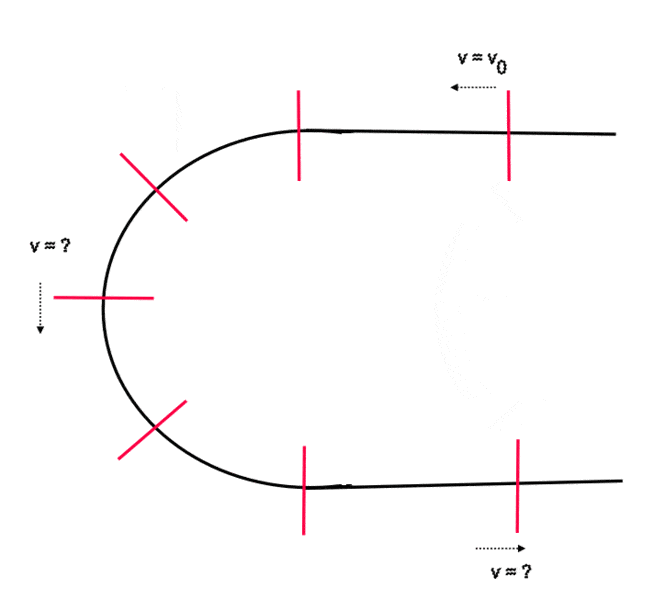
as per the attached graphics, assume a thin rigid rod of length L and mass m moving frictionless constrained to a rail such that is always locally perpendicular to the latter. The rod starts off with speed v=v0 in the straight path of the rail. My question is, what is the speed in the apex of the curved section (half a circle with radius R), and what is the speed after it is in the straight section again? There are no external forces acting.
Thanks.
