Curvatures at Surface point for non-normal planes

[Soulagenda]

I hope I am able to formulate this question properly as I am not extremely versed in differential geometry.

I have an arbitrary 3d smooth surface, S, defined by discrete points and their respective normal, N. I also have an arbitrary vector, V, pointing at that surface. I need the min and max principal curvatures,κ_min and κ_max, at a point, P, from the curves, L, formed by the intersection of the arbitrary surface and a plane, Q, which V lies on and rotates about V. So let θ be the angle between N and V, γ be the angle of rotation of Q about V in the clockwise direction.

Please refer to the picture below to get a better illustration of the problem.

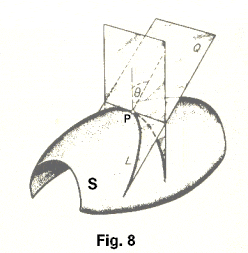
Is there a generic formula for such a problem out there. I haven't ran across anything as of yet.

 

[Mandelbroth]

defined by discrete points

Please clarify this.

 

[Soulagenda]

Discrete points meaning the (x, y, z) coordinates. So the surface is not defined by a function like z=f(x,y) but instead as a set of x(i,j), y(i,j) and z(i,j).

 

[Mandelbroth]

Discrete points meaning the (x, y, z) coordinates. So the surface is not defined by a function like z=f(x,y) but instead as a set of x(i,j), y(i,j) and z(i,j).

As in a finite set?

Do you see why I'm not understanding your thinking? You can't determine a unique surface with only a finite number of points.

 

[Soulagenda]

No, the initial surface data is given as a point cloud. I can get surface info such as slopes, the normal at points and such using numerical techniques. I haven't found any numerical techniques for determining curvature or second derivatives of interest on a surface. I just need the relationships to go from what I have which is a surface in the form of points and their respective normals to get the curvature of interest.
So, I was hoping that I could find someone familiar with an analytical approach that I can use. The analytical solution to the problem I stated will help greatly. Even if one defines the surface as a known function.

 

[Mandelbroth]

No, the initial surface data is given as a point cloud.

I'm unfamiliar with what you mean here. I've never heard the term "point cloud." Again, I don't see how you are attempting this because either you have some finite set of points or you have a relation defining where the points go, which means a chart can be constructed with relative ease. It's not clear what we have to work with here.

 

[Soulagenda]

Well thank you for considering to provide some assistance with my problem. You can google point cloud and get an idea of what it is.
The solution for the picture I presented is on this website: http://www.solitaryroad.com/c326.html. However, it does not show or have a relationship for when the plane Q rotates about vector V at various angles. That's what I'm looking for. I'm hoping there's an extension of the equation that accounts for the rotation of Q.

 

[Mandelbroth]

Well thank you for considering to provide some assistance with my problem. You can google point cloud and get an idea of what it is.
The solution for the picture I presented is on this website: http://www.solitaryroad.com/c326.html. However, it does not show or have a relationship for when the plane Q rotates about vector V at various angles. That's what I'm looking for. I'm hoping there's an extension of the equation that accounts for the rotation of Q.

I have looked up the term point cloud. Wikipedia defines it as "a set of data points in some coordinate system." It sets no bound on the cardinality of the points. Additionally, it does give several ways of turning a point cloud into a surface, but these methods will NOT provide a unique smooth surface with a finite number of points. They will only produce one of many possible surfaces. Do you see why?

There are several approaches that I can think of trying. Our curve $L$ is just the locus $\{x\in\mathbb{R}^3:x\in Q\cap S\}$, right? If we parametrized it, we should be able to get some unit tangent vectors.

 

[Soulagenda]

Yes I see why the points alone do not define a unique surface but along with the normals and a condition of smoothness, I believe it minimizes the possible surfaces. However, determining the surface is not my problem.

Your last statement is right on the nose. I'm trying to figure out how to get from the tangent vectors to curvature. I'm speculating that all curvatures at a point have a relationship with the rate of change of the Normals along two intersecting curves on the surface. with the intersection point being the point of interest.

 

[Chestermiller]

Yes I see why the points alone do not define a unique surface but along with the normals and a condition of smoothness, I believe it minimizes the possible surfaces. However, determining the surface is not my problem.

Your last statement is right on the nose. I'm trying to figure out how to get from the tangent vectors to curvature. I'm speculating that all curvatures at a point have a relationship with the rate of change of the Normals along two intersecting curves on the surface. with the intersection point being the point of interest.

I can see what you are trying to do. Consider x, y, and z to be continuous functions of i and j. Let $\vec{r}$ be a position vector from the origin to a point on the surface. Then a differential position vector within the surface is given by:

$$d\vec{r}=\vec{a}_idi+\vec{a}_jdj$$

where $\vec{a}_i$ and $\vec{a}_j$ are coordinate basis vectors within the surface, given by:

$\vec{a}_i=\frac{\partial \vec{r}}{\partial i}$

$\vec{a}_i=\frac{\partial \vec{r}}{\partial j}$

The normal to the surface is given by:
$$\vec{n}=\frac{\vec{a}_i\times \vec{a}_j}{\vert \vec{a}_i\times \vec{a}_j \vert}$$
The curvature tensor is equal to the 2D intrasurface gradient of the normal:
$$\vec{κ}=∇\vec{n}=\vec{a}^i\frac{\partial \vec{n}}{\partial i}+\vec{a}^j\frac{\partial \vec{n}}{\partial j}$$
where $\vec{a}^i$ and $\vec{a}^j$ are the reciprocal basis vectors.

 

[Chestermiller]

Was my response of any help. I can provide additional details if you'd like. I have actual real world practical experience with this exact kind of thing.

Chet

 

[Soulagenda]

I can see what you are trying to do. Consider x, y, and z to be continuous functions of i and j. Let $\vec{r}$ be a position vector from the origin to a point on the surface. Then a differential position vector within the surface is given by:

$$d\vec{r}=\vec{a}_idi+\vec{a}_jdj$$

where $\vec{a}_i$ and $\vec{a}_j$ are coordinate basis vectors within the surface, given by:

$\vec{a}_i=\frac{\partial \vec{r}}{\partial i}$

$\vec{a}_i=\frac{\partial \vec{r}}{\partial j}$

The normal to the surface is given by:
$$\vec{n}=\frac{\vec{a}_i\times \vec{a}_j}{\vert \vec{a}_i\times \vec{a}_j \vert}$$
The curvature tensor is equal to the 2D intrasurface gradient of the normal:
$$\vec{κ}=∇\vec{n}=\vec{a}^i\frac{\partial \vec{n}}{\partial i}+\vec{a}^j\frac{\partial \vec{n}}{\partial j}$$
where $\vec{a}^i$ and $\vec{a}^j$ are the reciprocal basis vectors.

I apologize for the wait. I was in the midst of pondering on your response to see if it's really what I'm looking for. It seems to be a great starting point. I do have a few questions. Are your saying the divergence of the normal will give me the curvature? If so which curvature is this: mean curvature, principal, or another? If the curvature comes out as a tensor, how will I then go about using the components to extract a curvature relative to a particular plane and vector.

I was wondering if the reciprocal basis vector could be constructed to represent the intersecting plane of interest.

On another note, since you do have experience. Do you know if the principal curvatures as they relate to the rotation of a normal plane is equivalent to the min and max curvatures from a non-normal rotational plane at the same point.

 

[Chestermiller]

I apologize for the wait. I was in the midst of pondering on your response to see if it's really what I'm looking for. It seems to be a great starting point. I do have a few questions. Are your saying the divergence of the normal will give me the curvature?

No. The gradient of the normal gives you the curvature tensor. You can then resolve this tensor into its principal components.

If the curvature comes out as a tensor, how will I then go about using the components to extract a curvature relative to a particular plane and vector.

This is really easy. You just dot the curvature tensor with a differential position vector within the surface, and divide by the length of the differential position vector.

I was wondering if the reciprocal basis vector could be constructed to represent the intersecting plane of interest.

I'm not sure what the intersecting plane of interest means. But, the reciprocal basis vectors can be determined in terms of a linear combination of the coordinate basis vectors. They lie within the surface, and satisfy the equations:

$$\vec{a}^k\centerdot \vec{a}_l=δ_l^k$$

On another note, since you do have experience. Do you know if the principal curvatures as they relate to the rotation of a normal plane is equivalent to the min and max curvatures from a non-normal rotational plane at the same point.

Sorry. Don't understand this question.

 

[Soulagenda]

Thank you for that explanation things are starting to clear up.

I'm not sure what the intersecting plane of interest means.

On another note, since you do have experience. Do you know if the principal curvatures as they relate to the rotation of a normal plane is equivalent to the min and max curvatures from a non-normal rotational plane at the same point.

Sorry. Don't understand this question.

Sorry for my self-made terminology. Let me explain.

For example, if you take a sphere centered at the origin with a radius of R. At any point on that sphere, if you construct a plane that the normal lies on, the intersection will result in a circle with a radius of R. I refer to these planes as 'normal planes' and they can vary with a rotation about the normal vector.

Now if instead of rotating a plane about the normal vector, you rotate a plane about an arbitrary vector. Let's say a vector that is parallel to the x-axis and offset h in the y-direction, where h<R. I referred to this plane as "non-normal rotational plane" and its intersection with the sphere will result in various circles with radii from R_h to R.

I am particularly interested in the second case where you have the vector parallel to the x-axis. From your statement

This is really easy. You just dot the curvature tensor with a differential position vector within the surface, and divide by the length of the differential position vector.

If I were looking for the min and max radii of curvatures in case 2. The point is P_h, the vector is (1, 0, 0) and the curvature tensor at P_h, is $\vec{κ}$_h. Will I simply do

$\vec{κ}$_h $\bullet$(1, 0, 0) = (κ_min, 0, κ_max)

R_h=1/κ_max and R=1/κ_min

Also does the principal curvature vector always have 0, κ_min and κ_max as its components? Or is it κ_x , κ_y and κ_z and the min and max have to be searched?

Or am I way off the mark with my perception of the differential position vector?

 

[Chestermiller]

Thank you for that explanation things are starting to clear up.




Sorry for my self-made terminology. Let me explain.

For example, if you take a sphere centered at the origin with a radius of R. At any point on that sphere, if you construct a plane that the normal lies on, the intersection will result in a circle with a radius of R. I refer to these planes as 'normal planes' and they can vary with a rotation about the normal vector.

Now if instead of rotating a plane about the normal vector, you rotate a plane about an arbitrary vector. Let's say a vector that is parallel to the x-axis and offset h in the y-direction, where h<R. I referred to this plane as "non-normal rotational plane" and its intersection with the sphere will result in various circles with radii from R_h to R.

I am particularly interested in the second case where you have the vector parallel to the x-axis. From your statement


If I were looking for the min and max radii of curvatures in case 2. The point is P_h, the vector is (1, 0, 0) and the curvature tensor at P_h, is $\vec{κ}$_h. Will I simply do

$\vec{κ}$_h $\bullet$(1, 0, 0) = (κ_min, 0, κ_max)

R_h=1/κ_max and R=1/κ_min

Also does the principal curvature vector always have 0, κ_min and κ_max as its components? Or is it κ_x , κ_y and κ_z and the min and max have to be searched?

Or am I way off the mark with my perception of the differential position vector?

I'm still a little confused, but maybe this will help.

The unit normal to the surface changes its orientation in space as you move from point to point along the surface. If $∇\vec{n}$ is the gradient of the unit normal with respect to position (within the surface), then if you dot $∇\vec{n}$ with a differential position vector $\vec{dr}$ in some direction within the surface (at the same point where $∇\vec{n}$ is specified), you get the change in the unit normal vector between the two adjacent points on the surface (defined by the differential position vector). The new unit normal vector at the end of the differential position vector may not lie in the plane formed by the original unit normal and the differential position vector. The change in the unit normal may have a component perpendicular to this plane. If that is the case, then the differential position vector $\vec{dr}$ is not a principal direction of curvature of the surface. On the other hand, if $∇\vec{n}\centerdot \vec{dr}$ is pointing in the same direction as $\vec{dr}$, then this is one of the two principal directions of curvature at the point. The other principal direction is perpendicular to this one (within the surface). In either case, if you dot the gradient of the unit normal (i.e., the curvature tensor) with a unit vector in one of the principal directions, you get back the unit vector times the magnitude of the principle curvature in that direction.

Now for case 2. It doesn't matter if the plane is perpendicular to the surface. In any case, it intersects the surface as a curve along the surface. At any point along this curve, you can identify a differential position vector along the curve. Once you do that, you are back to what we were doing in the previous paragraph.

Now, the curvature tensor at any point can be expressed in terms of the 4 dyadics involving combinations of the two coordinate basis vectors for the surface (at the point). However, since the two coordinate basis vectors can be expressed in terms of the unit vectors in the cartesian coordinate system, the curvature tensor at the same point can also be expressed in terms of the 9 diadics involving combinations of the 3 cartesian coordinate unit vectors. Thus, you can express the curvature tensor either way, and the two representations are entirely equivalent (since the curvature tensor is invariant to coordinate system). However, the version in terms of the coordinate basis vectors of the surface is much more meaningful, and much easier to work with.

Chet

 

[Chestermiller]

Since the OP has not responded to my last post in this thread, I have decided to flesh out the analysis I outlined in my previous posts, to demonstrate how one can determine the curvature tensor of the surface, given that the points on the surface are provided discretely. Any feedback and responses are welcome.

The spatial cartesian coordinates of points on the surface are represented parametrically in terms of the two coordinates i and j inscribed onto the surface as follows:

x = x(i,j)
y = y(i,j)
z = z(i,j)

where, even through i and j are descrete indices in your analysis, we now regard them as continuous parameters. In the present development, we also do not use the Einstein summation convention.

A differential position vector between two neighboring points within the surface is given by:
$$\vec{dr}=\vec{a_i}di+\vec{a_j}dj$$
where $\vec{a_i}$ and $\vec{a_j}$ are the coordinate basis vectors for the i,j coordinate system, given by:
$$\vec{a_i}=\frac{∂x}{∂i}\vec{i_x}+\frac{∂y}{∂i}\vec{i_y}+ \frac{∂z}{∂i}\vec{i_z}$$
$$\vec{a_j}=\frac{∂x}{∂j}\vec{i_x}+\frac{∂y}{∂j}\vec{i_y}+ \frac{∂z}{∂j}\vec{i_z}$$

If we dot the differential position vector with itself, we get the square of the distance between the two points (aka, the line element for the embedded coordinate system):
$$\vec{dr}\centerdot \vec{dr}=(dr)^2=g_{ii}(di)^2+2g_{ij}(di)(dj)+g_{jj}(dj)^2$$
where $$g_{ii}=\vec{a_i}\centerdot \vec{a_i}=(\frac{∂x}{∂i})^2+(\frac{∂y}{∂i})^2+(\frac{∂z}{∂i})^2$$
$$g_{ij}=\vec{a_i}\centerdot \vec{a_j}=(\frac{∂x}{∂i})(\frac{∂x}{∂j})+(\frac{∂y}{∂i})(\frac{∂y}{∂j})+(\frac{∂z}{∂i})(\frac{∂z}{∂j})$$
$$g_{jj}=\vec{a_j}\centerdot \vec{a_j}=(\frac{∂x}{∂j})^2+(\frac{∂y}{∂j})^2+(\frac{∂z}{∂j})^2$$
The reciprocal (or duel) basis vectors $\vec{a}^i$ and $\vec{a}^j$are defined by:
$$\vec{a}^i\centerdot \vec{a}_i=1$$
$$\vec{a}^i\centerdot \vec{a}_j=0$$
$$\vec{a}^j\centerdot \vec{a}_i=0$$
$$\vec{a}^j\centerdot \vec{a}_j=1$$
From these relationship, we can express the reciprocal basis vectors in terms of the coordinate basis vectors as follows:
$$\vec{a}^i=\frac{g_{jj}\vec{a}_i-g_{ij}\vec{a}_j}{(g_{ii}g_{jj}-g_{ij}^2)}$$
$$\vec{a}^j=\frac{g_{ii}\vec{a}_j-g_{ij}\vec{a}_i}{(g_{ii}g_{jj}-g_{ij}^2)}$$
The unit normal to the surface is given by:
$$\vec{n}=\frac{\vec{a_i}\times \vec{a_j}}{\vert \vec{a_i}\times \vec{a_j}\vert}$$
where
$$\vec{a_i}\times \vec{a_j}=\left(\frac{∂y}{∂i}\frac{∂z}{∂j}-\frac{∂z}{∂i}\frac{∂y}{∂j}\right)\vec{i_x}+\left(\frac{∂z}{∂i}\frac{∂x}{∂j}-\frac{∂x}{∂i}\frac{∂z}{∂j}\right)\vec{i_y}+\left(\frac{∂x}{∂i}\frac{∂y}{∂j}-\frac{∂y}{∂i}\frac{∂x}{∂j}\right)\vec{i_z}$$
$$\vert\vec{a_i}\times \vec{a_j} \vert=D=\sqrt{\left(\frac{∂y}{∂i}\frac{∂z}{∂j}-\frac{∂z}{∂i}\frac{∂y}{∂j}\right)^2+\left(\frac{∂z}{∂i}\frac{∂x}{∂j}-\frac{∂x}{∂i}\frac{∂z}{∂j}\right)^2+\left(\frac{∂x}{∂i}\frac{∂y}{∂j}-\frac{∂y}{∂i}\frac{∂x}{∂j}\right)^2}$$
The curvature tensor is obtained by taking the gradient of the unit normal vector:
$$\vec{κ}=∇\vec{n}=\vec{a}^i\frac{∂\vec{n}}{∂i}+\vec{a}^j\frac{∂\vec{n}}{∂j}$$
The change in the unit normal vector between coordinates (i,j) and (i+di, j+dj) is given by:
$$d\vec{n}=∇\vec{n}\centerdot (\vec{a_i}di+\vec{a_j}dj)=(\vec{a}^i\frac{∂\vec{n}}{∂i}+\vec{a}^j\frac{∂\vec{n}}{∂j})\centerdot (\vec{a_i}di+\vec{a_j}dj)$$
But,
$$\frac{∂\vec{n}}{∂i}\centerdot \vec{a_i}=\vec{a}^i(\frac{∂\vec{n}}{∂i}\centerdot \vec{a_i})\centerdot \vec{a_i}$$
$$\frac{∂\vec{n}}{∂j}\centerdot \vec{a_i}=\vec{a}^i(\frac{∂\vec{n}}{∂j}\centerdot \vec{a_i})\centerdot \vec{a_i}$$
$$\frac{∂\vec{n}}{∂i}\centerdot \vec{a_j}=\vec{a}^j(\frac{∂\vec{n}}{∂i}\centerdot \vec{a_j})\centerdot \vec{a_j}$$
$$\frac{∂\vec{n}}{∂j}\centerdot \vec{a_j}=\vec{a}^j(\frac{∂\vec{n}}{∂j}\centerdot \vec{a_j})\centerdot \vec{a_j}$$
If we substitute these four relationships into the previous equation, we obtain:
$$d\vec{n}=∇\vec{n}\centerdot (\vec{a_i}di+\vec{a_j}dj)=\left(\vec{a}^i\vec{a}^i(\frac{∂\vec{n}}{∂i} \centerdot \vec{a_i})+\vec{a}^i\vec{a}^j(\frac{∂\vec{n}}{∂i}\centerdot\vec{a_j})+ \vec{a}^j\vec{a}^i(\frac{∂\vec{n}}{∂j}\centerdot \vec{a_i})+\vec{a}^j\vec{a}^j(\frac{∂\vec{n}}{∂j}\centerdot \vec{a_j})\right)\centerdot (\vec{a_i}di+\vec{a_j}dj)$$
From this, it follows that the curvature tensor is given by:
$$\vec{κ}=∇\vec{n}=(\frac{∂\vec{n}}{∂i} \centerdot \vec{a_i})\vec{a}^i\vec{a}^i+ (\frac{∂\vec{n}}{∂i}\centerdot\vec{a_j})\vec{a}^i\vec{a}^j+ (\frac{∂\vec{n}}{∂j}\centerdot \vec{a_i})\vec{a}^j\vec{a}^i+(\frac{∂\vec{n}}{∂j}\centerdot \vec{a_j})\vec{a}^j\vec{a}^j$$
Since the unit normal vector $\vec{n}$ is perpendicular to the coordinate basis vectors $\vec{a_i}$ and $\vec{a_j}$, the previous expression for the curvature tensor can also be written in a more convenient form involving the partial derivatives of the coordinate basis vectors as:
$$\vec{κ}=∇\vec{n}=-\left((\frac{∂\vec{a_i}}{∂i} \centerdot \vec{n})\vec{a}^i\vec{a}^i+ (\frac{∂\vec{a_j}}{∂i}\centerdot\vec{n})\vec{a}^i\vec{a}^j+ (\frac{∂\vec{a_i}}{∂j}\centerdot \vec{n})\vec{a}^j\vec{a}^i+(\frac{∂\vec{a_j}}{∂j}\centerdot \vec{n})\vec{a}^j\vec{a}^j\right)$$

Suppose that θ represents the angle between the coordinate basis vectors $\vec{a}_i$ and $\vec{a}_j$ at each point on the surface. Then,
$$\vec{a}_i \centerdot \vec{a}_j=g_{ij}=\vert \vec{a}_i \vert \vert \vec{a}_j \vert \cosθ=\sqrt{g_{ii}g_{jj}}\cosθ$$
Therefore,
$$\sqrt{g_{ii}g_{jj}-g_{ij}^2}=\vert \vec{a}_i \vert \vert \vec{a}_j \vert \sinθ$$
But,
$$\vert \vec{a}_i \vert \vert \vec{a}_j \vert \sinθ=\vert \vec{a}_i \times \vec{a}_i \vert=D$$
Therefore,
$$\sqrt{g_{ii}g_{jj}-g_{ij}^2}=D$$
So, finally, we have:
$$\vec{κ}=∇\vec{n}=κ_{ii}\vec{a}^i\vec{a}^i+κ_{ij}(\vec{a}^i\vec{a}^j+ \vec{a}^j\vec{a}^i)+κ_{jj}\vec{a}^j\vec{a}^j$$
where
$$κ_{ii}=-\frac{∂\vec{a}_i}{∂i}\centerdot \vec{n}$$
$$κ_{ij}=-\frac{∂\vec{a}_i}{∂j}\centerdot \vec{n}=-\frac{∂\vec{a}_j}{∂i}\centerdot \vec{n}$$
$$κ_{jj}=-\frac{∂\vec{a}_j}{∂j}\centerdot \vec{n}$$
These represent the covariant components of the curvature tensor.

This completes what I wanted to present.

Chet