Normal modes and degree of liberty

[quasar987]

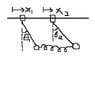
I have a book here that says that the number of normal modes is equal to the number of degree of freedom of a system. I'm wondering if this applies to just about any system or only to systems in which every coordinates can oscillate harmonically. The question is not very well formulated, so I included a picture. (The support of the pendulums can slide along the horizontal line)

This system has 4 degrees of freedom. Does it have 2 or 4 normal modes of oscillations?

 

[HackaB]

What book are you using, if you don't mind my asking? I think the coordinates have to be able to oscillate harmonically for the term "normal mode" to apply.

Are the masses of all the blocks the same? I'm not even sure if that matters, I'm just curious.

 

[quasar987]

Hi HackaB,

The book is 'The Physics of Waves' by Georgi. Very bad.

I invented the example.. so let's say the masses are the same.

 

[HackaB]

That is a very hard book, but you probably don't need me to tell you that. See if you can find a copy of "Waves" by Crawford at your library.

I did some research, and it turns out that your system has four normal modes even if the masses are different. So yes, an oscillatory system with n degrees of freedom has n normal modes. In the normal modes, the masses all oscillate with the same frequency and are in phase (or exactly pi out of phase).

But like you said, let's consider the case where all the masses are the same. If you introduce the new coordinates x_3 and x_4:

x_3 = L * theta_1
x_4 = L * theta_2

Label the blocks 1 thru 4, accordingly. Each has mass m.

Then you work out the K matrix that gives the restoring force (per unit displacement) on block i due to a displacement x_j of block j, and set up Newton's equation

$$M \ddot{X} = KX$$

where X is the column vector (x_1, ... , x_4) and M is just the matrix with m's on the diagonal and zeros everywhere else. Multiplying by M^-1 gives

$$\ddot{X} = M^{-1}KX$$

Solving this system amounts to finding the eigenvalues and eigenvectors of $M^{-1}K$. In this special case, since the masses are all equal, $M^{-1}K$ is a symmetric matrix. That means that its eigenvectors are orthogonal. That is why I asked whether the masses were the same, because I was thinking that the eigenvectors corresponding to the normal modes had to be orthogonal. But they don't.

I haven't worked it out, but I *think* you might find that one of the natural frequencies is zero. That corresponds to the boring case of all four masses moving together in one direction at a constant speed--a translational motion of the whole system. But that still counts as a normal mode.

 

[shyboy]

I think that is just a mathematical fact. In general you may linearize any system, so you have a set of linear equations, and you solve it to find normal modes. Evidently the number of modes will be equal to the original number of degrees of freedom.
If the system in some weird state where you cannot linearize it, or the determinant iz zero, you have a special point. That may have something to do with Luiville(?) theorem, but I am not so sure about that.

 

[quasar987]

The caracteristic equation that allows us to find the normal frequencies is

$$\det (M^{-1}K - I\omega ^2)=0$$

What guarentees us that it has n distinct solutions for $\omega ^2$?

I would also ask what guarentees that they are all real, and all positive but Georgi's book answers that one.

 

[HackaB]

What guarentees us that it has n distinct solutions for ?

Nothing. It is possible to have degenerate frequencies--that is, multiple normal modes with the same frequency.

 

[HackaB]

In general you may linearize any system, so you have a set of linear equations, and you solve it to find normal modes.

You have to linearize about a stable equilibrium to get real frequencies. So I don't know if the term "normal modes" applies to a general system, which may not have stable equilibria.

 

[quasar987]

Nothing. It is possible to have degenerate frequencies--that is, multiple normal modes with the same frequency.

Hmm, yes. So my question should be more: "Given any number of normal frequencies $\omega_i ^2$, what guarentees that the total number of (linearly independant) normal modes is n, the number of degree of freedom?"

Is there a theorem that says that "if m is the multiplicity of an eigenvalue $\lambda$ in the caracteristic equation, then the eigenspace associated to it is of dimension m"?

 

[HackaB]

First, I should point out that I defined the K matrix incorrectly--it should be defined the negative of what I defined it, so that the matrix equation is

$$M \ddot{X} = -KX$$

which makes it consistent with the one dimensional equation

$$m \ddot{x} = -kx$$

Is there a theorem that says that "if m is the multiplicity of an eigenvalue in the caracteristic equation, then the eigenspace associated to it is of dimension m"?

According to Georgi, in the next to last paragraph on p 74, this statement is true because K is symmetric and the masses are positive. So it apparently is a theorem for this type of system, but he does not prove it mathematically.

 

[quasar987]

First, I should point out that I defined the K matrix incorrectly--it should be defined the negative of what I defined it, so that the matrix equation is

$$M \ddot{X} = -KX$$

which makes it consistent with the one dimensional equation

$$m \ddot{x} = -kx$$



According to Georgi, in the next to last paragraph on p 74, this statement is true because K is symmetric and the masses are positive. So it apparently is a theorem for this type of system, but he does not prove it mathematically.

Cool. I'll ask about it in the math section. Thanks for the help HackaB.

 

[HackaB]

That sounds like a good idea. If you find out anything interesting, post it here. I'd like to know more about it myself.

edit: I see now that you meant the math section of PF. In that case I can look at the responses myself

 

[quasar987]

pp.61, in proving that $K_{jk}=K_{kj}$ Georgi argues that there is a potential function V that satisfies

$$F_j = -\frac{\partial{V}}{dx_j}$$

for any j. Got any idea what that potential energy function is?

The function

$$V(x_1,x_2,...,x_n) = \sum_{j=1}^{n} \sum_{k>j}^{n}K_{jk}x_jx_k + \sum_{j=1}^{n}\frac{1}{2}K_{jj}x_j^2$$

works, provided we know a priori that $K_{jk}=K_{kj}$. But we want a potential function that allows us to conclude to that quality. (see equ. 3.18)

 

[HackaB]

Well, I don't have the book nearby, but I'll take a guess at it. The potential function can be any function that has a second order minimum--that is, the first derivatives vanish at a point (call it x = 0) but not all of the second derivatives do. So what this equation

$$V(x_1,x_2,...,x_n) = \sum_{j=1}^{n} \sum_{k>j}^{n}K_{jk}x_jx_k + \sum_{j=1}^{n}\frac{1}{2}K_{jj}x_j^2$$

represents is the Taylor series for V carried out to second order, which is all you need for small oscillations. The $K_{jk}$ represent the second derivatives evaluated at x = 0:

$$K_{jk} = \frac{\partial^2 V}{\partial x_j \partial x_k}(0,...,0) = \frac{\partial^2 V}{\partial x_k \partial x_j}(0,...,0) = K_{kj}$$

since partial derivatives commute. So the K_jk 's are symmetric. That is why in the Taylor expansion above, they have taken the 1/2 off the first sum and only summed over k > j.

edit: in the Taylor series, the zeroth order (constant) term V_0 has been set to zero, since an overall offset in the potential function doesn't change the motion any.

 

[quasar987]

Got it.

---------