- #1
- 23,093
- 7,499
Quick question. If the EM field vectors are perpendicular to the direction that an EM wave is traveling, how can light push objects away from the light source, such as in the use of a solar sail?
nsaspook said:
vanhees71 said:If the wave packet travels in good approximation in a single direction (i.e., if the spatial Fourier spectrum is sharply peaked around a wave vector [itex]\vec{k}[/itex], you can show that the total momentum of the wave packet is mostly into the direction of [itex]\vec{k}[/itex].
nsaspook said:
Drakkith said:Quick question. If the EM field vectors are perpendicular to the direction that an EM wave is traveling, how can light push objects away from the light source, such as in the use of a solar sail?
Drakkith said:Thanks, but I'm afraid I don't quite understand. Can you elaborate a bit on how this answers my question?
Starting with Maxwell's theory, we are naturally led to consider the problem: How does the energy about an electric current pass from point to point — that is, by what paths and according to what law does it travel from the part of the circuit where it is first recognisable as electric and magnetic to the parts where it is changed into heat or other forms?
The aim of this paper is to prove that there is a general law for the transfer of energy, according to which it moves at any point perpendicularly to the plane containing the lines of electric force and magnetic force, and that the amount crossing unit of area per second of this plane is equal to the product of the intensities of the two forces, multiplied by the sine of the angle between them, divided by 4\pi, while the direction of flow of energy is that in which a right-handed screw would move if turned round from the positive direction of the electromotive to the positive direction of the magnetic intensity. After the investigation of the general law several applications will be given to show how the energy moves in the neighbourhood of various current-bearing circuits.
...
I have therefore given several cases in considerable detail of the application of the mode of transfer of energy in current-bearing circuits according to the law given above, as I think it is necessary that we should realize thoroughly that if we accept Maxwell's theory of energy residing in the medium, we must no longer consider a current as something conveying energy along the conductor. A current in a conductor is rather to be regarded as consisting essentially of a convergence of electric and magnetic energy from the medium upon the conductor and its transformation there into other forms. The current through a seat of so-called electromotive force consists essentially of a divergence of energy from the conductor into the medium. The magnetic lines of force are related to the circuit in the same way throughout, while the lines of electric force are in opposite directions in the two parts of the circuit — with the so-called current in the conductor, against it in the seat of electromotive force. It follows that the total E.M.I. round the circuit with a steady current is zero, or the work done in carrying a unit of positive electricity round the circuit with the current is zero. For work is required to move it against the E.M.I. in the seat of energy, this work sending energy out into the medium, while an equal amount of energy comes in in the rest of the circuit where it is moving with the E.M.I. This mode of regarding the relations of the various parts of the circuit is, I am aware, very different from that usually given, but it seems to me to give us a better account of the known facts.
KatamariDamacy said:It says: ...E and B are always perpendicular to each other and the direction of propagation... and their time and position dependences are:
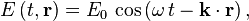
Both E and B fields are three-dimensional or volumetric, uniformly so.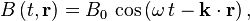
How then they can be "perpendicular" to anything, especially E field with its spherical symmetry?
What are those unique directions or vectors of E and B fields that are perpendicular, what defines them?
jtbell said:What do you mean by "volumetric" here?
There is no spherical symmetry here. These are standard equations for a plane wave.
The vector ##\vec k## points in the direction of propagation. ##\vec E## and ##\vec B## are each perpendicular to ##\vec k##. ##\vec E## and ##\vec B## are also perpendicular to each other. These perpendicularity conditions are not contained in the two equations above, but are specified separately. They follow from the requirement that ##\vec E## and ##\vec B## must satisfy Maxwell's equations. See for example this page:
http://farside.ph.utexas.edu/teaching/em/lectures/node48.html
specifically equations (445), (446) and (448).
Orodruin said:At each point in space, the E field has a direction and a magnitude and so does the B field.
The difference between a red and a blue EM wave is the frequency, not the direction. A blue EM wave has a high frequency and a red EM wave has a low frequency. If you trace a ray from the blue/red object to the eye then the E and B fields of that wave will both be perpendicular to that ray and also perpendicular to each other at every point along the path. The eye does not distinguish polarization, but if the wave is vertically polarized then the E field will be vertical and the B field horizontal, and vice versa if the wave is horizontally polarized.KatamariDamacy said:What's the magnitude of E field in EM wave of color red, for example? Same as in blue EM wave?
At each point the E field has a magnitude and a direction. At each point the B field has a magnitude and a direction. They are vector fields. That is what it means for a field to be a vector field. There is no special name given to the direction of the fields, but they have one at each point nonetheless.KatamariDamacy said:I know about velocity, acceleration, force or momentum direction, what direction of E and B fields are you talking about, can you name it? What is it, what defines it?
ChrisVer said:If for example your wave propagates along the z-axis (that is [itex]\hat{k}=\hat{z}[/itex]) then the E,B fields will be on the xy plane (E might have x and B might have y...)
DaleSpam said:The difference between a red and a blue EM wave is the frequency, not the direction. A blue EM wave has a high frequency and a red EM wave has a low frequency. If you trace a ray from the blue/red object to the eye then the E and B fields of that wave will both be perpendicular to that ray and also perpendicular to each other at every point along the path. The eye does not distinguish polarization, but if the wave is vertically polarized then the E field will be vertical and the B field horizontal, and vice versa if the wave is horizontally polarized.
At each point the E field has a magnitude and a direction. At each point the B field has a magnitude and a direction. They are vector fields. That is what it means for a field to be a vector field. There is no special name given to the direction of the fields, but they have one at each point nonetheless.
Orodruin said:At each particular point, the E field points in the direction it is pointing.
No. For visible light the magnitude is related to the brightness. The brighter the light the greater the magnitude.KatamariDamacy said:Do you confirm then the magnitude of E and B fields is the same for every EM wave?
Please read the material provided and ask questions about the material.KatamariDamacy said:At each point from where, is magnitude relative to distance, squared? Yes, vector fields are three-dimensional and have infinitely many directions, that is vectors, one at each any arbitrary point in space. So, if at each point the E field has a magnitude and a direction, then which one of all those directions do you call "the direction", and what's unique about it?
Orodruin said:Just as a central field is a possible solution to Maxwell's equations, corresponding to a point charge, EM waves are also a solution, corresponding to an EM wave in free space with the E and B field perpendicular to the direction of propagation.
DaleSpam said:No. For visible light the magnitude is related to the brightness. The brighter the light the greater the magnitude.
Please read the material provided and ask questions about the material.
ChrisVer said:1 dimensional vector= number...
A vector field:
http://mathworld.wolfram.com/VectorField.html
(fast definition)
http://en.wikipedia.org/wiki/Vector_field
KatamariDamacy said:What do you think is their geometry? Do you think E and B are three-dimensional fields, or some kind of one-dimensional vectors, or what?
Nugatory said:This is a question that you could only ask if either you still haven't looked at Maxwell's equations, or if you've looked and didn't understand what any of the symbols in them mean.
If the latter, speak up and may be able to steer you towards the right introductory texts.
ChrisVer said:Why are you asking what I think?
The definition given by the Wolfram is satisfying ,,, they are vectors:
[itex] \vec{E}(t,x,y,z)= (E_{x}(t,x,y,z),E_{y}(t,x,y,z),E_{z}(t,x,y,z)) [/itex]
[itex] \vec{B}(t,x,y,z)= (B_{x}(t,x,y,z),B_{y}(t,x,y,z),B_{z}(t,x,y,z)) [/itex]
KatamariDamacy said:So those blue and red vectors are "field variations". Variations in what? Position, magnitude, direction, momentum, velocity, force ...?