- #1
Rectifier
Gold Member
- 313
- 4
1. The problem
There are four charges hat are placed in a rectangle-like pattern. Three of them are equal (A, B, D).
What charge should C be so that the net force at charge B is zero?
2. Relevant information
(No distances are given)
3. The attempt
First of all, I did this image to visualize the problem.
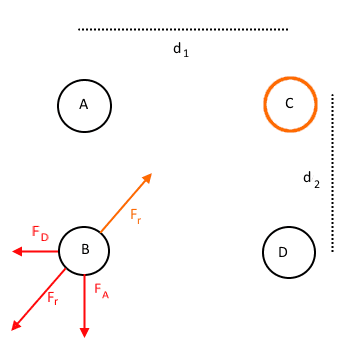
Charge A affects B with a force ## F_A ##. Charge D affects B with a force ## F_D ##. ## F_r ## is the resultant force of ## F_A ## and ## F_D ##.
I define the distance between ##AC=CA=DB=BD## to be equal to ##d_1##. The distance between ##CD=DC=AB=BA## is then equal to ##d_2##. Distance between ##BC=CB## can be derived from ##d_1## and ##d_2## with the help of the Pythagorean equation.
$$ d_3^2=d_1^2+d_2^2 $$
What we can see here is that the charge C must affect A with a force that has an equal magnitude but opposite direction to ## F_r ##. Hence
$$ F_{r} -F_{r}=0 $$
The force that affect these charges can be formulated with the help of Coulomb's law.
$$F=k \frac{Q_1 \cdot Q_2}{d^2} $$
This leads to following equations for the force that is affecting charge B$$F_D= k\frac{Q^2}{d_1^2}\\ F_A = k\frac{Q^2}{d_2^2} \\ F_{r}= k\frac{Q \cdot Q_c}{d_3^2}$$
The relationship between ##F_A##, ##F_D## and ##F_r## can be written with the help of the Pythagorean equation
$$ \\ F_{r}^2= F_D^2+F_A^2 $$
On this stage, I insert the equation for ##d_3^2## inside ##F_r## (force from C) and insert ##F_r, F_A## and ##F_D## into the equation for ##F_r## described by Pythagorean equation.
$$\\ F_{r}= k\frac{Q \cdot Q_c}{d_1^2+d_2^2} \\ (k\frac{Q \cdot Q_c}{d_1^2+d_2^2})^2 = (k\frac{Q^2}{d_1^2})^2+(k\frac{Q^2}{d_2^2} )^2 \\ $$
And here is where it gets crazy:
$$(k\frac{Q \cdot Q_c}{d_1^2+d_2^2})^2 = (k\frac{Q^2}{d_1^2})^2+(k\frac{Q^2}{d_2^2} )^2\\ (\frac{Q_c}{d_1^2+d_2^2})^2 = (\frac{Q}{d_1^2})^2+(\frac{Q}{d_2^2})^2 \\ Q_c^2 =( (\frac{Q}{d_1^2})^2+(\frac{Q}{d_2^2})^2 ) \cdot (d_1^2+d_2^2)^2 \\ Q_c^2 =Q^2 \frac{d_1^4+d_2^4}{(d_1d_2)^4} \cdot (d_1^2+d_2^2)^2$$
And here is the place that I am stuck on. I don't think it is possible to simplify it more.
Have I missed something?
Please help me. :,(
There are four charges hat are placed in a rectangle-like pattern. Three of them are equal (A, B, D).
What charge should C be so that the net force at charge B is zero?
2. Relevant information
(No distances are given)
3. The attempt
First of all, I did this image to visualize the problem.
Charge A affects B with a force ## F_A ##. Charge D affects B with a force ## F_D ##. ## F_r ## is the resultant force of ## F_A ## and ## F_D ##.
I define the distance between ##AC=CA=DB=BD## to be equal to ##d_1##. The distance between ##CD=DC=AB=BA## is then equal to ##d_2##. Distance between ##BC=CB## can be derived from ##d_1## and ##d_2## with the help of the Pythagorean equation.
$$ d_3^2=d_1^2+d_2^2 $$
What we can see here is that the charge C must affect A with a force that has an equal magnitude but opposite direction to ## F_r ##. Hence
$$ F_{r} -F_{r}=0 $$
The force that affect these charges can be formulated with the help of Coulomb's law.
$$F=k \frac{Q_1 \cdot Q_2}{d^2} $$
This leads to following equations for the force that is affecting charge B$$F_D= k\frac{Q^2}{d_1^2}\\ F_A = k\frac{Q^2}{d_2^2} \\ F_{r}= k\frac{Q \cdot Q_c}{d_3^2}$$
The relationship between ##F_A##, ##F_D## and ##F_r## can be written with the help of the Pythagorean equation
$$ \\ F_{r}^2= F_D^2+F_A^2 $$
On this stage, I insert the equation for ##d_3^2## inside ##F_r## (force from C) and insert ##F_r, F_A## and ##F_D## into the equation for ##F_r## described by Pythagorean equation.
$$\\ F_{r}= k\frac{Q \cdot Q_c}{d_1^2+d_2^2} \\ (k\frac{Q \cdot Q_c}{d_1^2+d_2^2})^2 = (k\frac{Q^2}{d_1^2})^2+(k\frac{Q^2}{d_2^2} )^2 \\ $$
And here is where it gets crazy:
$$(k\frac{Q \cdot Q_c}{d_1^2+d_2^2})^2 = (k\frac{Q^2}{d_1^2})^2+(k\frac{Q^2}{d_2^2} )^2\\ (\frac{Q_c}{d_1^2+d_2^2})^2 = (\frac{Q}{d_1^2})^2+(\frac{Q}{d_2^2})^2 \\ Q_c^2 =( (\frac{Q}{d_1^2})^2+(\frac{Q}{d_2^2})^2 ) \cdot (d_1^2+d_2^2)^2 \\ Q_c^2 =Q^2 \frac{d_1^4+d_2^4}{(d_1d_2)^4} \cdot (d_1^2+d_2^2)^2$$
And here is the place that I am stuck on. I don't think it is possible to simplify it more.
Have I missed something?
Please help me. :,(
Last edited: