- #1
stratman
- 3
- 0
Set + Number = "Sumber"
Set+Number = "Sumber"
The content of this thread is based on ideas proposed in the Complementary Association Theory, which was posted in several threads in this forum by Organic.
Consider the following computation task:
Given a graphical representation of an Element, comprised of n sub-elements. How many transitional states are there from the initial state where all n sub-elements are indistinguishable to the final state where each sub-element can be uniquely identified?
For an Element comprised of 1 sub-element the task is simple, there is exactly one state. For example given an "arc" representation model, the graphic representation of this state would be:
http://62.219.145.154/s1.png
For an Element comprised of 2 sub-elements, there are two transitional states. In the initial state we have 2 indistinguishable sub-elements, and in the final state we make one sub-element uniquely identifiable by marking it with an underline:
http://62.219.145.154/s2.png
For an Element comprised of 3 sub-elements, there are three transitional states. In the initial state, again we have 3 indistinguishable sub-elements, then in the second state, we associate two sub elements into one, by drawing an arc around them and thereby making them uniquely identified. In the third and final state we make one of the sub elements in the associated twin sub-elements uniquely identified by underlining it:
http://62.219.145.154/s3.png
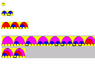
For an Element comprised of 4 sub-elements, there are 9 transitional states:
http://62.219.145.154/s4.png
For any n > 0, the following algorithm calculates the number of transitional states:
ASSOCIATION_LEVEL(int n):Vector
1 V© new vector
2 if n = 1 then
3 V©V + the single root of level 1
4 if n = 2 then
5 V©V + the two roots of level 2
6 else
7 if n >2 then do
8 For each partition vector P in n do:
9 ROOTS(P,V)
10 return V
ROOTS(vector P,vector V)
1 roots ©[]
2 for each element in P do:
3 if element is a root then
4 roots© roots + element
5 else
6 roots©ASSOCIATION_LEVEL(integer value of element)
7 return horizontal alignment of the Cartesian product of P and draw new arc around them
When considering the graphical representation of a compound element comprised of n sub-elements, one may find properties in this element which belong to sets, as the ability to contain other elements. Also, properties that belong to numbers can be identified in these elements, properties as quantity and order. But, there are also properties that can be found in neither numbers nor sets, the most important one is structure.
I am interested in learning what applications if any can be applied to these compound structured elements.
Stratman.
P.S. I have implemented a small Java Applet, grphically displaying all states for elements until n=8, as you see this function grows quite rapidly, and this computation depends on the power/memory of the running computer. For those interested I can send this Applet.
Set+Number = "Sumber"
The content of this thread is based on ideas proposed in the Complementary Association Theory, which was posted in several threads in this forum by Organic.
Consider the following computation task:
Given a graphical representation of an Element, comprised of n sub-elements. How many transitional states are there from the initial state where all n sub-elements are indistinguishable to the final state where each sub-element can be uniquely identified?
For an Element comprised of 1 sub-element the task is simple, there is exactly one state. For example given an "arc" representation model, the graphic representation of this state would be:
http://62.219.145.154/s1.png
For an Element comprised of 2 sub-elements, there are two transitional states. In the initial state we have 2 indistinguishable sub-elements, and in the final state we make one sub-element uniquely identifiable by marking it with an underline:
http://62.219.145.154/s2.png
For an Element comprised of 3 sub-elements, there are three transitional states. In the initial state, again we have 3 indistinguishable sub-elements, then in the second state, we associate two sub elements into one, by drawing an arc around them and thereby making them uniquely identified. In the third and final state we make one of the sub elements in the associated twin sub-elements uniquely identified by underlining it:
http://62.219.145.154/s3.png
For an Element comprised of 4 sub-elements, there are 9 transitional states:
http://62.219.145.154/s4.png
For any n > 0, the following algorithm calculates the number of transitional states:
ASSOCIATION_LEVEL(int n):Vector
1 V© new vector
2 if n = 1 then
3 V©V + the single root of level 1
4 if n = 2 then
5 V©V + the two roots of level 2
6 else
7 if n >2 then do
8 For each partition vector P in n do:
9 ROOTS(P,V)
10 return V
ROOTS(vector P,vector V)
1 roots ©[]
2 for each element in P do:
3 if element is a root then
4 roots© roots + element
5 else
6 roots©ASSOCIATION_LEVEL(integer value of element)
7 return horizontal alignment of the Cartesian product of P and draw new arc around them
When considering the graphical representation of a compound element comprised of n sub-elements, one may find properties in this element which belong to sets, as the ability to contain other elements. Also, properties that belong to numbers can be identified in these elements, properties as quantity and order. But, there are also properties that can be found in neither numbers nor sets, the most important one is structure.
I am interested in learning what applications if any can be applied to these compound structured elements.
Stratman.
P.S. I have implemented a small Java Applet, grphically displaying all states for elements until n=8, as you see this function grows quite rapidly, and this computation depends on the power/memory of the running computer. For those interested I can send this Applet.
Attachments
Last edited by a moderator: