Dependent variables Definition and 23 Threads
-

Euler-Lagrange Equation for Several Dependent Variables
Homework Statement [/B] Homework Equations $$f_u- \frac{d}{dx} \left(f_{u'} \right) = 0 $$ $$f_v- \frac{d}{dx} \left(f_{v'} \right) = 0 $$ The Attempt at a Solution So I calculated the following, if someone could check what I've done it would be greatly appreciated, but I'm not convinced...- CMJ96
- Thread
- Dependent variables Euler-lagrange Variables
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

A RK method for heat equation with dependent variables
Hello. How do I solve this equation without killing the k(y) term: I managed to derive an analytical solution for this one. I intend to run the numerical solution via Runge-Kutta but I can't stop myself from killing the k(y) term. I'm starting to think I'm doing something wrong... It goes...- maistral
- Thread
- Dependent variables Heat Heat equation Method Variables
- Replies: 1
- Forum: Differential Equations
-
D
I Difficulty with function dependencies f(u,x)
If you have a function x = x(u,t) then does u necessarily depend on x and t? so u = (x,t) For example, if x(u,t)=u^2 t it seems that because t=x/u^2 , t=t(x,u) I am having difficulty working out the general equation for dz \over dx if z=z(x,y,t) x=x(u,t) y=y(u,v,t) The chain rule...- D O
- Thread
- Dependent variables Differentiation Difficulty Function Multivariable Partial derivative
- Replies: 7
- Forum: General Math
-
Dependent and independent variables exercise: the basics | Algebra I | Khan Academy
Here we have a problem that asks us to identify which variables are dependent and independent. Hint: independent variables are not influenced and remain unch...- RooksAndBooks
- Media item
- algebra i dependent variables independent variables khan academy sal khan
- Comments: 0
- Category: Basic Algebra
-
Dependent and independent variables exercise: graphing the equation | Algebra I | Khan Academy
It's helpful to express an equation on a graph where we plot at least 2 points. Watch and we'll show you. Practice this lesson yourself on KhanAcademy.org ri...- RooksAndBooks
- Media item
- algebra i dependent variables independent variables khan academy sal khan
- Comments: 0
- Category: Basic Algebra
-
Dependent and independent variables exercise: express the graph as an equation | Khan Academy
We're flipping the last video on its head and doing the opposite. This time we give you the graph and ask you to express it as an equation. Practice this les...- RooksAndBooks
- Media item
- algebra i dependent variables independent variables khan academy sal khan
- Comments: 0
- Category: Basic Algebra
-
S
[Statistics] Independent vs. Dependent Variables
Hi everyone I have a quick question about independent and dependent variables. Homework Statement The following data set gives the number of miles traveled, and the travel time in hours for each of the 10 car's driving assignments. Miles Time 90 9 40 5 90 9 90...- statisticsquestion
- Thread
- Dependent variables Independent Statistics Variables
- Replies: 2
- Forum: Precalculus Mathematics Homework Help
-
S
I Calculus of Variations Dependent variables and constraints
If we have a function: \begin{equation} f(x,x',y,y',t) \end{equation} and we are trying to minimise this subject to a constraint of \begin{equation} g(x,x',y,y',t) \end{equation} Would we simply have a set of two euler lagrange equations for each dependent variable, here we have x and y...- shedrick94
- Thread
- Calculus Calculus of variations Constraints Dependent variables Variables
- Replies: 1
- Forum: General Math
-

Are q and q' dependent variables in Lagrangian or not?
Hi. I have thought that the variables q and q' in L = L(q, q') are independent. (q' = dq/dt) Of course q and q' are functions of time t , but they are only dependent in terms of t . However, in the sight of general(or abstract? I mean, not specific) functional L(q, q'), q and q' are just...- DOTDO
- Thread
- Dependent variables Lagrangian Variables
- Replies: 1
- Forum: Classical Physics
-
L
Error propagation with dependent variables
Homework Statement Based on Microdosimetry theory, trying to figure out error propagation for a lot of quantities that are produced from radiation spectra. I am having trouble finding information on how to calculate and propagate errors when the quantities in my equations are not independent...- lachy
- Thread
- Dependent variables Error Error propagation Propagation Uncertainty Variables
- Replies: 2
- Forum: Advanced Physics Homework Help
-
D
Jointly continuous random dependent variables
Homework Statement Let X and Y be rv's with joint pdf f(x,y) = 6(1-y) for 0≤x≤y≤1 and 0 elsewhere find Pr(X≤3/4, Y≤1/2) Homework Equations The Attempt at a Solution Ok I am having trouble with finding the right limits of integration for dependent variables. If we let the...- DotKite
- Thread
- Continuous Dependent variables Random Variables
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
O
MHB Joint cumulative distribution of dependent variables
Hello everyone! The problem: $X,Y,Z$ are random variables that are dependent and uniformly-distributed in $[0,1]$, and let $\alpha$ be a given number in $[0,1]$. I am asked to compute the following: $\text{Pr}(X+Y+Z>\alpha \;\;\; \& \;\;\; X+Y\leq \alpha)$ What I have so far...- OhMyMarkov
- Thread
- Dependent variables Distribution Joint Variables
- Replies: 5
- Forum: Set Theory, Logic, Probability, Statistics
-
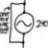
Covariance of two dependent variables
Homework Statement See figure attached Homework Equations The Attempt at a Solution I am not concerned with part (a), I have deduced that indeed X and Y are dependent. I'm not sure if I have done part (b) correctly, and I am quite certain I have done part (c) incorrectly, but...- jegues
- Thread
- Covariance Dependent variables Variables
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
A
Paritial derivative of function of dependent variables
i am having a hard time understanding partial derivative for function of dependent variables. for example let's consider $$z=x+y$$ so by usual steps that are mentioned on e.g wikipedia etc. $$\frac{\partial}{\partial x}z=1$$ but what if its also true that $$y=x$$ (or in other words... -
H
Identifying Independent and Dependent Variables
Hi, I am trying to identify the independent and dependent variables in the following experiment: Two groups of patients (Epileptic and Normal) are exposed to varying wavelengths of light and their neural response is quantified and recorded. I am using...- HAL10000
- Thread
- Dependent variables Independent Variables
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
V
Weak convergence of the sum of dependent variables, question
Hi guys, Problem: Let {Xn},{Yn} - real-valued random variables. {Xn}-->{X} - weakly; {Yn}-->{Y} weakly. Assume that Xn and Yn - independent for all n and that X and Y - are independent. Fact that {Xn+Yn}-->{X+Y} weakly, can be shown using characteristic functions and Levy's theorem...- vovchik
- Thread
- Convergence Dependent variables Sum Variables Weak
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-
V
Question on how to assure randomness for a set of dependent variables
Hello all, Please excuse my naive question that follows. I do not have much experience in Statistics and need to obtain a set of variables which assures randomness in the variables. From central limit theorem, I believe addition of random independent variables assures randomness of the...- venvidu
- Thread
- Dependent variables Randomness Set Variables
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
C
Partial derivatives with dependent variables (fixed) question.
In statistical mechanics we express partial derivatives of functions, keeping some variables fixed. But these variables are functions of the other variables (which are not fixed). I'm just confused by this, what is the convention for taking these derivatives? For example, if we have S as a...- Curl
- Thread
- Dependent variables Derivatives Partial Partial derivatives Variables
- Replies: 3
- Forum: General Math
-
A
Expected value of random sums with dependent variables
Hi all, I have a question of computing the expectation of random sums. E(sim_{k=1}^N X_k) = E(N)E(X) if N and X_1, X_2,...are independent and X_k's are iid. Here both N and X_k's are r.vs. But the condition of N and X_1, X_2,...being independent is not true in many cases. How will...- agarwalv
- Thread
- Dependent variables Expected value Random Sums Value Variables
- Replies: 5
- Forum: Set Theory, Logic, Probability, Statistics
-
D
Independent and Dependent Variables
I'm doing a lab where i need to calculate the heat energy, or enthalpy using the equation (delta) H = m x c x T my reactions are going to be of a strong acid and a strong base: Sulfuric Acid + Sodium Hydroxide→ Sodium Sulfate + Water and of a wek acid and the same strong base...- ditto_299
- Thread
- Dependent variables Independent Variables
- Replies: 1
- Forum: Biology and Chemistry Homework Help
-
J
How to Handle PDEs with Two Dependent Variables?
That's right, I said dependent. Does anyone have any experience dealing with such beasts. I haven't been able to find a single mention of them in any textbook on PDEs. The thing I'm really curious to know is whether the method of separation of variables works as usual, e.g. if the dep vars...- jdstokes
- Thread
- Dependent variables Pde Variables
- Replies: 2
- Forum: Differential Equations
-
P
Independent / Dependent variables for implicit functions
This probably has a really simple answer. Forr u=x^2-y^2 and v=x^2+y^2 x and y are apparently the dependent variables. But the independent variable is the input while the dependent variable is the output, so since u=f1(x,y) and v=f2(x,y) shouldn't they (u and v) be the dependent variables? -
W
Solving a Trig Question: Identifying Independent & Dependent Variables
Here is a trig question that I've been thinking about. I want to know which one would be the independant and the dependant of the points (r , theta)- WillyTech
- Thread
- Dependent variables Independent Trig Variables
- Replies: 1
- Forum: Precalculus Mathematics Homework Help


