Gaussian distribution Definition and 67 Threads
-
C
I What Is the Probability Atom A Will Emit a Photon Before Atom B?
For concretness I'll use atoms and photons but this problem is actually just about probabilities. There's an atom A whose probability to emit a photon between times t and t+dt is given by a gaussian distribution probability P_A centered around time T_A with variance V_A. There's a similar atom...- Capitano
- Thread
- Gaussian distribution Probability distribution Probability theory Statistics
- Replies: 4
- Forum: Set Theory, Logic, Probability, Statistics
-
M
I Grating Resolving Power of Laser Beams with Gaussian Distribution
All resources I’ve found for grating resolving power assume uniform distribution on the grating and produce airy disks. Resolvance is determined by the Rayleigh criterion where the peak of one wavelength is at the minima of the adjacent one. This definition doesn’t seem applicable for Gaussian... -
J
B Sigma Multiplied Gaussian Distribution
Hi! Say i have two variables that have independent gaussian distributions of probability of being a certain value when i sample them, what is the likely hood that both will land on a 3 sigma value simultaneously? Is there an equation that easily determines that? Also for other combinations like...- jaydnul
- Thread
- Distribution Gaussian Gaussian distribution Sigma
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
P
Understanding the meaning of "expected fraction" (Statistics)
The first part of the question asked me to calculate the mean and standard deviation for the number of remain votes in the simple binomial model consisting of total sample size of 2091 people. I believe this is fairly straightforward, it was simply ##E(X) = \mu = 2091(0.5) = 1045.5## votes and...- ProbablySid
- Thread
- Binomial distribution Expectation value Fraction Gaussian distribution Standard deviation Statistics
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
B
I A few questions about doing a Gaussian Fit
A few questions about doing a Gaussian Fit : 1) Is gaussian fit and gaussian regression the same thing ? 2) I have a gaussian function that will return a list of gaussian numbers giving an initial list length. So if you input 5 you will get: 1,2,6,4,1. My question is if I have an image and I...- btb4198
- Thread
- Fit Fitting Gaussian Gaussian distribution
- Replies: 4
- Forum: Linear and Abstract Algebra
-
F
A Try to swap between mean and partial derivatives on a product
- fab13
- Thread
- Chi-squared Covariance matrix Derivatives Fisher information Gaussian distribution Maximum likelihood Mean Partial Partial derivatives Product
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-

I Can a Gaussian distribution be represented as a sum of Dirac Deltas?
We know that Dirac Delta is not a function. However, I just talk about the numerical version of it that we use every day. We can simply represent the Dirac delta function as a limiting case of Gaussian distribution when the width of the distribution ##\sigma->0##. $$ \delta(x - \mu) =...- tworitdash
- Thread
- Dirac Distribution Gaussian Gaussian distribution Sum
- Replies: 2
- Forum: General Math
-

Mutual Information from this Gaussian Distribution
Let us suppose we are given a Gaussian Distribution in the form of $$p(x,y) \propto exp(-\frac{1}{2}x^2 - \frac{1}{2}by^2 - cxy)$$ What are the equations that I need to use to obtain Mutual Information ?- Arman777
- Thread
- Distribution Gaussian Gaussian distribution Information
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

A What is the Derivation of the Inverse Gaussian Distribution by Schrödinger?
Could you help me about the derivation of inverse gaussian distribution? During my search I encountered that it was derived by schrödinger as a result of differential equation solution but I can not find his derivation on internet...- mertcan
- Thread
- Distribution Gaussian Gaussian distribution Inverse
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-

Probability from the tolerance of a capacitor (Gaussian distribution)
Given the upper data, if the nominal value for capacitance is 33nF and tolerance of 20%, then values can range between 26.4nF and 39.6nF. With the bottom margin being set at 30nF, this means that the interval takes approximately 72% of all values. Is this the correct procedure to solve this...- Peter Alexander
- Thread
- Capacitor Distribution Gaussian distribution Probability Tolerance
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
K
Deconvolution of fluorescence spectra
I am trying to make a deconvolution of fluorescence spectra in Matlab. The original spectra is the yellow graph in the figure below. The other two graphs are Cauchy distributions, x and y, that I have manually added to the plot. I would like to write a program that could do this automatically...- Kristoffer Linder
- Thread
- Deconvolution Fluorescence Gaussian distribution Spectra
- Replies: 1
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
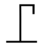
What is the integral of this Gaussian distribution?
Homework Statement Find A in p(x) = Aexp(-λ(x-a)^2) by using the equation 1 = ∫ p(x)dxHomework Equations 1 = ∫p(x)dx The Attempt at a Solution I expand the power of the exponential and then extract the constant exponential to get: Aexp(λa^2) ∫exp(-λx^2)exp(2aλx)dx I don't know how to...- Boltzman Oscillation
- Thread
- Distribution Gaussian Gaussian distribution Integral
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
A
I Sampling from a multivariate Gaussian distribution
I was watching a lecture on youtube about linear regression and there's a section where it had the statement below (written in purple). Does multiplying by sigma rotate the distribution to make it look like x - N(mew, sigma^2)? Mew in this case is 0 so it doesn't shift the distribution.- asilvester635
- Thread
- Distribution Gaussian Gaussian distribution Multivariate Sampling
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
D
I How does the distribution depend on a variable resolution
Dear all, We were trying to solve the following question but did not quite understand what to do. The question is as follows: The reconstructed invariant mass is usually described by a Gaussian (or Normal) distribution. However, the resolution σ (the width of the distribution) is found to...- Didier Drogba
- Thread
- Distribution Gaussian distribution Invariant mass Resolution Standard deviation Statistic Variable
- Replies: 4
- Forum: Set Theory, Logic, Probability, Statistics
-
A
I Negative values for Gaussian Distribution
So in my Physics lab, we divided into groups and our task was to throw darts on a target containing 13 bins. The bins look something like the image below. At the end, our class combined our average, standard deviation, and standard error. I made a Gaussian Distribution and I noticed that the...- aron silvester
- Thread
- Distribution Gaussian Gaussian distribution Negative
- Replies: 1
- Forum: Other Physics Topics
-

A Gaussian distribution characteristic function
Hello, guys. I am trying to solve for characteristic function of normal distribution and I've got to the point where some manipulation has been made with the term in integrands exponent. And a new term of t2σ2/2 has appeared. Could you be so kind and explain that to me, please... -
C
What is the Probability of Hereditary Conditions in a Gaussian Distribution?
Homework Statement Please help! I'm new to Gaussian and I've been on this problem for hours, I can't crack it at all (no pun intended) can anyone provide a detailed walk through the answers? On average 5% of eggs contain a hereditary condition. Use Gaussian distribution to find the...- conrad dunk
- Thread
- Distribution Gaussian Gaussian distribution Stats
- Replies: 8
- Forum: Precalculus Mathematics Homework Help
-
E
A Parameterizing conditional expectations (Gaussian case)
Consider three jointly normally distributed random variables X,Y and Z. I know that in the Gaussian case E[Z | X,=x Y=y]=xßZX;Y +yßZY;X where ßZX;Y notes the regression coefficient of Z on X conditional on Y (and ßZY;Xis analogously defined). Is the following derivation correct? E[Z| X>x...- estebanox
- Thread
- Conditional Conditional expectation Gaussian distribution
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
S
Error in summation of spectral components
HI everyone, Imagine we are sampling of a gaussian signal along time and need to know the power/variance associated with the first N spectral components. So we take our favorite fft algorithm to get the PSD. The error associated with a given estimated spectral component f(w) (w is the...- SpecGuest
- Thread
- Chi square Components Error Errors Gaussian distribution Summation
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
J
Integrating Gaussian Distribution (QM)
Homework Statement I am struggling with one of the end of chapter questions in my QM textbook (see attachment as I don't know how to show calculus on PF). It has thrown me because the chapter introduces some of the key principles in QM by talking about probability but then it randomly chucks in...- Jimmy87
- Thread
- Distribution Gaussian Gaussian distribution Qm
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
A
Determine the intensity profile and fwhm for gaussian beam.
Homework Statement A beam of wavelength 600 nm has initially an intensity profile of Gaussian shape with a fwhm of 1 mm. Determine the intensity profile and fwhm 10 meter away.Homework Equations FWHM = λ/(2NA√(1 + I/Is)) The Attempt at a Solution [/B] FWHM1 = 1mm = 600 nm/(2NA√(1 + I/Is))...- Aerozeppelin
- Thread
- Beam Fwhm Gaussian Gaussian beam Gaussian distribution Intensity Optics
- Replies: 5
- Forum: Advanced Physics Homework Help
-

Consider the Gaussian Distribution....?
Homework Statement Consider the Gaussian Distribution ## p(x) = Ae^{-\lambda(x-a)^{2}} ##, where ## A ##, ##a##, and ##\lambda## are constants. (Look up any integrals you need.) (a) Determine ##A## (I only need help with this (a)) Homework Equations ##\int_{-\infty}^{\infty} p(x)dx = 1##...- Destroxia
- Thread
- Distribution Gaussian Gaussian distribution
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Fortran [Fortran90]Problem with Gaussian distribution
Hi, I have a problem in my program and I cannot figure it out. In the last post I had a problem about some arrays, I perfectly resolved it thanks to you, but now my problem is a little bit subtle. I have a subroutine(here I'll post it has a program )that generates random numbers in order to...- Aner
- Thread
- Distribution Gaussian Gaussian distribution
- Replies: 8
- Forum: Programming and Computer Science
-

Fitting data to a Gaussian Distribution in Excel
Hey everyone, I'm hoping I can get some input on this. As some of you may recall, I'm currently in an internship at Fermilab, and I've hit a snag in plotting my data. I'm measuring the intensity of the NuMI neutrino beam at multiple different points to look for discrepancies in the measured...- QuantumCurt
- Thread
- Data Distribution Excel Fitting Gaussian Gaussian distribution
- Replies: 11
- Forum: MATLAB, Maple, Mathematica, LaTeX
-

Higgs mass - Why is it a Gaussian distribution?
Hi, so my question is along the lines of the following: If I'm looking at the decay channel H=>ZZ=>4 Muons, why would the resultant distribution for the mass of the parent Higgs be a Gaussian? Is it a case of the peak is the actual value of the Higgs at rest; those of greater mass are Higgs...- AlanKirby
- Thread
- Distribution Gaussian Gaussian distribution Higgs Mass
- Replies: 2
- Forum: High Energy, Nuclear, Particle Physics
-
J
Normal distribution starting with a uniformed distribution
Hi comunity! I need to make a code o a normal distribution of velocities, starting whit a random secuence uniformly distributed between [0,1]. I am using FNT95, with Plato. I want to obtain a ''for'' bucle with I=1,N for the velocities. It is importan for the distribution to have sigma defined...- Jamil
- Thread
- Code Distribution Fortran Gaussian distribution Initial conditions Initial state Normal Normal distribution
- Replies: 2
- Forum: Programming and Computer Science
-
F
Convergence of Integral with Real and Imaginary Parameters
The integral given below is to be computed as a function of real variables x and s. Even a partial answer only for s>0 is very useful. Here is the integral: $$\int_{0}^{\infty}{dk \frac{k^2 e^{-k^2 x^2}}{(k^2 + s)^{3/2}}}$$ Thank you for your help. -
2
How to Normalize the Quantum Harmonic Oscillator Wave Function?
when considering the quantum harmonic oscillator, you get that the wave function takes the form psi=ae^{-\frac{m\omega}{2\hbar}x^2} I have been trying to integrate \psi ^2 to find the constant a so that the wave function is normalised, and I know the trick with converting to polar coordinates...- 21joanna12
- Thread
- Distribution Energy levels Gaussian Gaussian distribution Harmonic oscillator Integral Normalization Quantum Wavefunction
- Replies: 3
- Forum: Calculus
-
T
Integration seems gaussian but the answer does not match
Homework Statement -h^2/2m (sqrt(2b/pi)) e^(-bx^2) d^2/dx^2 (e^(-bx^2)) dx from - to + infinity Homework Equations I tried differentiating e^(-bx^2) twice and it came up weird , I positioned the values and finally cam up with (-2b sqrt(pi/2b)...is there any other way to do it ? The...- tfhub
- Thread
- Gaussian Gaussian distribution Integration Match
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
G
Skewed Generalized Gaussian Distribution
I am looking for more information (e.g., reference, the CDF and descriptive stats) about a four-parameter skewed generalized Gaussian (SGG) distribution. I have come across the PDF for this distribution, but with no reference and not a lot of other information. Here is a snippet... On...- geo101
- Thread
- Distribution Gaussian Gaussian distribution generalized Probability density
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
C
Calculate the standard deviation of Gaussian distribution ,thanks
Given a one-dimensional Gaussian distribution, distributed as following: f (x) = exp (-x ^ 2 / (2q)) / q / √ (2pi) proof which q is the standard deviation Thanks !The standard deviation is defined by: http://www.mathsisfun.com/data/standard-deviation-formulas.html- chener
- Thread
- deviation Distribution Gaussian Gaussian distribution Standard Standard deviation
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
L
Gaussian Distrib: What is Standard Deviation of Mean?
In my course textbook it is written that "approximately 68% of the measurements from a normally distributed set lie within +-1 standard deviation of the mean value". What do they mean by standard deviation of the mean value? They give a definition for "the mean"(of a set of measurements(data))...- lover-of-light
- Thread
- Distribution Gaussian Gaussian distribution
- Replies: 3
- Forum: Set Theory, Logic, Probability, Statistics
-

What is the RMS deviation from the true mean for a Gaussian distribution?
Hi everyone, I'm new here and this is my first post in this forum. ^^ Homework Statement Suppose that you observe a fluorescent object whose true location is x0. Individual photons come from this object with apparent locations xi in an approximately Gaussian distribution about x0...- cqfd
- Thread
- Distribution Gaussian Gaussian distribution Rms
- Replies: 16
- Forum: Advanced Physics Homework Help
-
C
Gaussian distribution other than standard form
what changes does there occur in the result of the gaussian distribution "integration e^-alpha*x^2 dx=sqrt(pi/alpha) if i substitute that x^2 with some (x-a)^2? then what should be the integral result ? -
C
Problems with Gaussian distribution
Homework Statement consider this Gaussian distribution p(x)=Ae^-(a(x-b)^2) Homework Equations use integration p(x)dx=1 to find out the value of A The Attempt at a Solution hi, i know about the gaussian distribution formula integration e^-alpha*x^2 = sqrt(pi/alpha) now for...- cooper607
- Thread
- Distribution Gaussian Gaussian distribution
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
X
What's the difference between Bell curve and Gaussian distribution
I was looking to the definition of the Bell curve, and the Gaussian distribution, but I don't see any difference when we represent them in a graph. Both have the same Bell curve. What is the difference between the Bell curve and the Gaussian distribution?- xeon123
- Thread
- Bell Curve Difference Distribution Gaussian Gaussian distribution
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
S
Exponential of Gaussian Distribution
I'm looking for the expected value of an exponential Gaussian Y=\text{exp}(jX) \text{ where } X\text{~}N(\mu,\sigma^2) From wolframalpha, http://www.wolframalpha.com/input/?i=expected+value+of+exp%28j*x%29+where+x+is+gaussian E[Y]=\text{exp}(j^2\sigma^2/2+j\mu) If I were to use the...- SeriousNoob
- Thread
- Distribution Exponential Gaussian Gaussian distribution
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
S
Changing the Gaussian Distribution from cartesian to polar coordinates
Homework Statement "You are now going to show that, in the Gaussian distribution P(x)=Ae^(-Bx^2) the constant A is equal to sqrt(B/Pi). Do this by insisting that the sum over probabilities must equal unity, Integral(P(x)dx)=1. To make this difficult integral easier, frst square it then combine...- stepheckert
- Thread
- Cartesian Coordinates Distribution Gaussian Gaussian distribution Polar Polar coordinates
- Replies: 1
- Forum: Advanced Physics Homework Help
-
E
Continous Time Gaussian Distribution
Hello all, I have the following equation \mathbf{v}(t)=\mathbf{P}(t)\mathbf{d}+\mathbf{w}(t) where v(t) is a 2-by-1 vector, P(t) is 2-by-2N matrix, d is a 2N-by-1 vector, and w(t) is an 2-by-1 Gaussian process vector where each element is of zero mean and variance N0. What is the probability...- EngWiPy
- Thread
- Distribution Gaussian Gaussian distribution Time
- Replies: 7
- Forum: Set Theory, Logic, Probability, Statistics
-

Derivation of the Antiderivative of the Gaussian Distribution
I'm in a high school pre-calculus class and a statistics class. For the latter, we are given z-tables for some of our tests. I don't like these z-tables. Thus, I decided that a more direct approach (fundamental theorem of calculus) would be more accurate and, more importantly, more fun. My...- Mandelbroth
- Thread
- Antiderivative Derivation Distribution Gaussian Gaussian distribution
- Replies: 5
- Forum: Calculus
-
A
Finding the Normalization Constant of a Gaussian Distribution (Griffiths 1.6)
Homework Statement Consider the Gaussian Distribution ρ(x) = A e^{-λ(x-a)^{2}} where A, a, and λ are constants. Determine the normalization constant A. Homework Equations \int^{∞}_{-∞}ρ(x) dx = 1 The Attempt at a Solution The problem recommends you look up all necessary integrals, so I...- ADCooper
- Thread
- Constant Distribution Gaussian Gaussian distribution Normalization
- Replies: 2
- Forum: Advanced Physics Homework Help
-
J
Intuitive explanations for Gaussian distribution function and mahalanobis distance
Hello I was wondering If anyone could give intuitive explanations for the multivariate Gaussian distribution function and mahalanobis distance? My professor didn't explain these in probability class, they were only defined... Where did the formula come from? Why is the Gaussian function the...- jjepsuomi
- Thread
- Distribution Distribution function Function Gaussian Gaussian distribution
- Replies: 8
- Forum: Set Theory, Logic, Probability, Statistics
-
P
Solving integral - gaussian distribution of cos
Homework Statement I have to prove: ∫(-infinity:infinity) cos(pi*v/2L)*e^-((L-L_av)^2/sqrt(2pi)*sigma^2) dL proportional to cos(pi*v/2L_av)*e^-(t/tau)^2 tau is some constant, and sigma << L_av. The Attempt at a Solution i can change the integral to 0:infinity, since sigma <<...- poul
- Thread
- Cos Distribution Gaussian Gaussian distribution Integral
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
M
Electron Cloud described by a Gaussian distribution
Homework Statement A cloud of electrons are drifting from a negative plate to a positive plate after being liberated by a laser pulse, (separated by a distance z = 10cm with an original potential difference of 15V) at an instant in time the centre of the cloud has traveled 25mm from the...- MrBeano
- Thread
- Cloud Distribution Electron Gaussian Gaussian distribution
- Replies: 1
- Forum: Advanced Physics Homework Help
-
J
Characteristic Function of Joint Gaussian Distribution
This is inspired by Kardar's Statistical Physics of Particles, page 45, and uses similar notation. Homework Statement Find the characteristic function, \widetilde{p}(\overrightarrow{k}) for the joint gaussian distribution: p(\overrightarrow{x})=\frac{1}{\sqrt{(2\pi)^{N}det...- Jolb
- Thread
- Characteristic Characteristic function Distribution Function Gaussian Gaussian distribution Joint
- Replies: 2
- Forum: Advanced Physics Homework Help
-
A
Bounded/Truncated Gaussian distribution
Dear all, I have a problem in understanding how to bound a Gaussian distribution. LEt me describe the problem at hand: Let's say that we have a Gaussian distribution in the x-coordinate and a Gaussian distribution in the y-coordinate. Further, assume that the independent random variables x...- architect
- Thread
- Distribution Gaussian Gaussian distribution
- Replies: 7
- Forum: Set Theory, Logic, Probability, Statistics
-
A
Show that a Gaussian Distribution Corresponds to a CTS random variable.
Going over my Lecture Notes my Lecturer as Started with Show that a Gaussian Distribution Corresponds to a CTS random variable. Then she has i) Taken the f(x) = [p.d.f] and shown a) f(x) >= 0 for all x member of real numbers. b) Integral over all real numbers = 1 ii) Found the M.G.F then...- andyb177
- Thread
- Distribution Gaussian Gaussian distribution Random Random variable Variable
- Replies: 1
- Forum: Set Theory, Logic, Probability, Statistics
-
V
What is the basic difference between Maxwell and Gaussian Distribution?
Can anyone tell me the basic difference between Maxwell and Gaussian distribution? Thanks in Advance- venkypunjabi
- Thread
- Difference Distribution Gaussian Gaussian distribution Maxwell
- Replies: 2
- Forum: Electromagnetism
-
X
Gaussian Distribution Question.
I am studying the Gaussian distribution and am doing one of the problems for practice. The problem states that the standard deviation is equal to 15 and the actual value recorded in the experiment is 385.0. It then asks what is the probability that a single measurement lies in the range of the...- Xyius
- Thread
- Distribution Gaussian Gaussian distribution
- Replies: 4
- Forum: Set Theory, Logic, Probability, Statistics
-
M
Sampling of a gaussian distribution
I have a 3d data cube. For every point I measure the property A which is a gaussian variable of mean m and variance s and it's also a function of the density d at every point. A(x,y,z)=f(d(x,y,z))e^(-(X-m)^2/(2\sigma^2)) X is a random number. Now let's say I want to sample the...- matteo86bo
- Thread
- Distribution Gaussian Gaussian distribution Sampling
- Replies: 1
- Forum: Calculus