Limit definition Definition and 58 Threads
-

B What is a general definition of a limit?
I suppose that it is because we are in extended real numbers. But the definition of a limit when ##x_0 = \infty## and let's say ##L=\infty## is different. Why are these definitions equivalent? Isn't the key that ##U_{\varepsilon}(\infty)=\left(\frac {1}{\varepsilon},\infty\right)##? -
Z
Spivak, Ch. 5 Limits, Problem 3 viii: Prove a limit of a function
Consider item ##vii##, which specifies the function ##f(x)=\sqrt{|x|}## with ##a=0## Case 1: ##\forall \epsilon: 0<\epsilon<1## $$\implies \epsilon^2<\epsilon<1$$ $$|x|<\epsilon^2\implies \sqrt{|x|}<\epsilon$$ Case 2: ##\forall \epsilon: 1\leq \epsilon < \infty## $$\epsilon\leq\epsilon^2...- zenterix
- Thread
- Calculus Function Limit Limit definition Limits Spivak
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-
R
I How can we define a limit approaching negative infinity?
I have the following definition: $$ \lim_{x\to p^+}f(x)=+\infty\iff \forall\,\,\varepsilon>0,\,\exists\,\,\delta>0,\,\,\text{with}\,\,p+\delta< b: p< x < p+\delta \implies f(x) > \varepsilon$$ From this, how can I get the definition of $$\lim_{x\to p^-}=-\infty? $$ -
R
MHB What is the definition of a negative infinity limit?
I have the following definition: $$\lim_{x\to p^+}f(x)=+\infty\iff \forall\,\,\varepsilon>0,\,\exists\,\,\delta>0,\,\,\text{with}\,\,p+\delta< b: p< x < p+\delta \implies f(x) > \varepsilon$$ From this, how can I get the definition of $$\lim_{x\to p^-}=-\infty? $$ -
G
MHB Derivative using the limit definition (without using L'Hospital's rule)
Hello everybody, could you help me with this problem please? I have to find a derivative in x0 of this function (without using L'Hospital's rule): I used the definition , but I don't know what to do next. Thank you.- goody1
- Thread
- Definition Derivative Limit Limit definition
- Replies: 4
- Forum: General Math
-

Evaluating the Limit of Cosine Function Using L'Hospital's Rule - Explained
<Moderator's note: Moved from a technical forum and thus no template.> $$\lim_{x \to 0} \cos(\pi/2\cos(x))/x^2$$ I tried to evaluate the limit this way, $$\lim_{x \to 0} \cos(\pi/2\cdot1)/x^2$$ since $$\cos0=1$$ $$\lim_{x \to 0} \cos(\pi/2\cdot1)/x^2=\lim_{x \to 0} 0/x^2$$ Now apply...- navneet9431
- Thread
- Calculus Limit Limit definition Partial
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

B Question about a limit definition
From Rosenlicht, Introduction to Analysis: Definition: Let E, E′ be metric spaces, let p0 be a cluster point of E, and let f(complement(p0)) be a function. A point q ∈ E" is called a limit of f at p0 if, given any e > 0, there exists a δ > 0 such that if p ∈ E , p < > p0 and d( p, p0) < δ... -

Reversed limit definition for monotonic functions
Homework Statement Does the delta-epsilon limit definition in reverse work for describing limits in monotonic functions? By reversed, one means for lim (x -> a) f(x) = L if for each δ there corresponds ε such that 0 < | x-a | < δ whenever | f(x) - L | < ε. Homework EquationsThe Attempt at...- ecoo
- Thread
- Definition Functions Limit Limit definition
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
M
Ε-δ proof: lim x->a f(x) = lim h->0 f(a + h)
This is a simple exercise from Spivak and I would like to make sure that my proof is sufficient as the proof given by Spivak is much longer and more elaborate. Homework Statement Prove that \lim_{x\to a} f(x) = \lim_{h\to 0} f(a + h) Homework EquationsThe Attempt at a Solution By the...- MeyCey
- Thread
- Calculus 1 Epsilon delta Epsilon delta proof Limit Limit definition Proof
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
S
I Why Must Epsilon Be Greater Than Zero in Sequence Limits?
in the limit definition of a sequence, why does epsilon has to be greater than 0 and not greater or equal to 0? thanks in advance. -

Rigorous Multivariable Limit Definition Problem
Homework Statement Hey I'm trying to prove the rigorous definition of limit for the following function: Lim (x,y) approaches (1,1) of f(x,y)=(y*(x-1)^(4/3))/((x/1)^2+abs(x)*y^2) Homework Equations abs(x^2)<abs(x^2 +y^2) The Attempt at a Solution I know the rigorous definition of limit. I...- dumbdumNotSmart
- Thread
- Definition Limit Limit definition Multivariable Rigorous Vector calculus
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
&
I How to understand the notion of a limit of a function
I am trying to explain to someone the formal notion of a limit of a function, however it has made me realize that I might have some faults in my own understanding. I will write down how I understand the subject and would very much appreciate if someone(s) can point out any...- "Don't panic!"
- Thread
- Derivative Function Intuition Limit Limit definition
- Replies: 8
- Forum: Calculus
-

A multivariable limit problem (epsilon-delta -proof)
Homework Statement Find the limit \lim_{(x,y)\to(2,2)}\frac{x^3-y^3}{x-y} Homework Equations \epsilon - \delta, baby: If the limit L exists, \forall \: \epsilon \: \exists \: \delta: 0 < \sqrt{(x-a)^2+(y-b)^2} < \delta \rightarrow |f(x,y)-L| < \epsilon The Attempt at a Solution By...- TheSodesa
- Thread
- Epsilon delta proof Limit Limit definition Multivariable Multivariable calculus Proof
- Replies: 15
- Forum: Calculus and Beyond Homework Help
-
S
Finding derivative of x^x using limit definition
I am trying to find the derivative of x^x using the limit definition and am unable to follow what I have read. Can someone help me understand why lim [(x+h)^h -1]/h as h ---> 0 = ln(x). This part of the derivatio- scottshannon
- Thread
- Definition Derivative Limit Limit definition
- Replies: 2
- Forum: Calculus
-
H
Limit Definition of Indefinite Integrals?
Hello, I was just wondering, we have what could be called the indefinite derivative in the form of d/dx x^2=2x & evaluating at a particular x to get the definite derivative at that x. But with derivation, we can algebraically manipulate the limit definition of a derivative to actually evaluate...- hddd123456789
- Thread
- Definition Indefinite Integrals Limit Limit definition
- Replies: 6
- Forum: General Math
-
A
MHB Question about minimum function and limit definition (proper)
Hi, Suppose you want to prove $|x - a||x + a| < \epsilon$ You know $|x - a| < (2|a| + 1)$ You need to prove $|x + a| < \frac{\epsilon}{2|a| + 1}$ So that $|x - a||x + a| < \epsilon$ Why does Michael Spivak do this: He says you have to prove --> $|x + a| < min(1, \frac{\epsilon}{2|a| +...- Amad27
- Thread
- Definition Function Limit Limit definition Minimum
- Replies: 5
- Forum: Topology and Analysis
-
E
A new limit definition of integral?
I think i discovered a new way to define an integral, i don't know if it helps in any particular case, but its an idea worth posting i think. The idea is to define the height of the rectangles based on one single point of the function and then build up the next heights for the other rectangles...- EzequielJC
- Thread
- Definition Integral Limit Limit definition
- Replies: 5
- Forum: Calculus
-
P
Question about limit definition of partial derivative
I've seen it written two different ways: $$\frac{\partial f}{\partial x} = \lim\limits_{h \rightarrow 0} \frac{f(x + h, y) - f(x,y)}{h}$$ and $$\frac{\partial f}{\partial x} = \lim\limits_{h \rightarrow 0} \frac{f(x_0 + h, y_0) - f(x_0,y_0)}{h}$$ where the latter evaluates the function at...- PNutMargarine
- Thread
- Definition Derivative Limit Limit definition Partial Partial derivative
- Replies: 1
- Forum: Calculus
-
G
Limit definition to compute some complex value function
So there is something I don't understand in the definition of limit that is applied to some problem I have some intuition for like the rigorous limit definition but I don't have full understanding when applied to some problems. Use definition 2 to prove lim as z → i of z^2 = -1 The...- Genericcoder
- Thread
- Complex Definition Function Limit Limit definition Value
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
F
Application on the limit definition of e
Application on the limit definition of "e" Hi, I have known that: (i) (1+\frac{a}{n})^n=((1+\frac{a}{n})^\frac{n}{a})^a\to e^a (ii) (1-\frac{1}{n})^n=(\frac{n-1}{n})^n=(\frac{1}{\frac{n}{n-1}})^{(n-1)+1}=(\frac{1}{1+\frac{1}{n-1}})^{(n-1)}\cdot (\frac{1}{1+\frac{1}{n-1}}) \to \frac{1}{e}\cdot... -
V
Limit Definition Derivative: e^(-1/x)
Homework Statement Let f(x) =\begin{cases} 0 & \text{ if } x\leq 0 \\ e^\left ( -1/x \right ) & \text{ if } x> 0 \end{cases} Compute f'(x) for x < 0 and x > 0. Homework Equations f'(x) = \lim \ \ \ \ \ \ \displaystyle{\frac{e^{(-1/(x+h)} - e^{-1/x}}{h}} \\ \ \ \ \ \ \ \ \ \...- Vale132
- Thread
- Definition Derivative Limit Limit definition
- Replies: 15
- Forum: Calculus and Beyond Homework Help
-
Q
Limit Definition of Derivative
Homework Statement http://i.minus.com/jbicgHafqNzcvn.png Homework Equations The limit definition of a derivative: [f(x+h)-f(x)]/h as h approaches zero is f'(x) The Attempt at a Solution I'm just not understanding the wording of the question. The limit given in the question is...- Qube
- Thread
- Definition Derivative Limit Limit definition
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
Q
Differentiability using limit definition
Homework Statement http://i.minus.com/jbzvT5rTWybpEZ.png Homework Equations If a function is differentiable, the function is continuous. The contrapositive is also true. If a function is not continuous, then it is not differentiable. A function is differentiable when the limit definition...- Qube
- Thread
- Definition Differentiability Limit Limit definition
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
P
Limit definition of derivative problem
Homework Statement Using the definition of derivative find f'(x) for f(x) = x - sqrt(x) Homework Equations None. The Attempt at a Solution lim h --> 0 : ((x + h) - sqrt(x + h) - x + sqrt(x))/h 1 - (sqrt(x + h) - sqrt(x))/h Multiply by conjugate.. 1 - h/(h*(sqrt(x) +...- physicsernaw
- Thread
- Definition Derivative Limit Limit definition
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
A
Limit definition and infinitely often
Limit definition and "infinitely often" If we have a sequence of real numbers x_{n} converging to x, that means \forall \epsilon > 0, \exists N such that |x_n - x| < \epsilon, \forall n \geq N. So, can we say P (|x_n - x| < \epsilon \ i.o.) = 1 because for n \geq N, |x_n - x| < \epsilon...- adnaps1
- Thread
- Definition Limit Limit definition
- Replies: 2
- Forum: Set Theory, Logic, Probability, Statistics
-
P
Use L'Hopital's Rule to relate to limit definition for e
Homework Statement It can be shown that lim n→∞(1 + 1/n)^n = e. Use this limit to evaluate the limit below. lim x→0+ (1 + x)^(1/x) Homework Equations The Attempt at a Solution So i guess what i need to do is try to get that limit in the form of the limit definition for e...- Painguy
- Thread
- Definition L'hopital's rule Limit Limit definition
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
M
Epsilon Delta Limit Definition
Homework Statement Prove lim x--> -1 1/(sqrt((x^2)+1) using epsilon, delta definition of a limit Homework Equations The Attempt at a Solution I know that the limit =(sqrt(2))/2 And my proof is like this so far. Let epsilon >0 be given. We need to find delta>0 s.t. if...- MathSquareRoo
- Thread
- Definition Delta Epsilon Epsilon delta Limit Limit definition
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
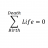
Multivariable limit definition question
Homework Statement I'm reading through Taylor's advanced calculus and came across this question in section 7.2 : http://gyazo.com/6b0c5a2e4e605ff77bf6584eb3295948 Homework Equations The definition of the partial of f with respect to some variable at some point (a,b), let's say the...- STEMucator
- Thread
- Definition Limit Limit definition Multivariable
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
S
Using Limit Definition of the Derivative?
If one uses the limit definition of a derivative (lim of (f(x)-f(a)) / (x-a)) as x approaches a) on a function and you get a value (ie. it is not undefined) does that mean the derivative of the function at that point exists? In other words, even if the limit definition of the derivative works...- SopwithCamel
- Thread
- Definition Derivative Limit Limit definition
- Replies: 2
- Forum: Calculus
-
S
Napier's Constant Limit Definition
Hi all ! I am terribly sorry if this was answered before but i couldn't find the post. So that's the deal. We all know that while x→∞ (1+1/x)^x → e But I am deeply telling myself that 1/x goes to 0 while x goes to infinity. 1+0 = 1 and we have 1^∞ which is undefined. But... -
F
Complex Limit Definition: Trying to Remember
Trying to remember how to use the definition of a complex limit. \lim_{\Delta z\to 0}\frac{f(z+h)-f(z)}{\Delta z} f(z) = |z| = \sqrt{x^2+y^2} \Delta z = \Delta x + i\Delta y \lim_{\Delta x\to 0}\frac{\sqrt{(x+\Delta x)^2+(y+\Delta y)^2}- \sqrt{x^2+y^2}}{\Delta x} Is that correct? Or do I...- fauboca
- Thread
- Complex Definition Limit Limit definition
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
S
Derivative of a^x using limit definition
Homework Statement Sketch and label on the same pair of axes the graphs of y=f(x) and y=f'(x) for ... c) f(x)=2x Homework Equations The Attempt at a Solution f(x) = 2x f'(x) = lim as h→0 (2x+h-2x)/h = lim as h→0 (2x2h-2x)/h = lim as h→0 2x(2h-1)/h = lim as h→0 2x ∙ lim as h→0 (2h-1)/h = 2x...- SithsNGiggles
- Thread
- Definition Derivative Limit Limit definition
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
A
Is this an accurate statement of the limit definition? (quantifiers/connectives)
\forall\epsilon\exists\delta[( (\epsilon\wedge\delta) > 0) \wedge ((| x - t| < \delta)\Rightarrow (|f(x) - f(t)|< \epsilon))] The part that seems wrong is the placement of the statement "delta is greater than zero" and "epsilon is greater than zero". It seems like these statements may need...- anonymity
- Thread
- Definition Limit Limit definition
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
R
Epsilon-delta limit definition trouble
Homework Statement Guess the limit and use the \epsilon-\delta definition to prove that your guess is correct. \lim_{x \to 9}\frac{x+1}{x^2+1}2. The attempt at a solution Guess limit to be \frac{10}{82}=\frac{5}{41} Therefore: |\frac{x+1}{x^2+1}-\frac{5}{41}| =...- rudders93
- Thread
- Definition Limit Limit definition
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
J
How Does the Epsilon-Delta Definition Prove a Limit Exists?
I know, I know, this topic has already been beat to death, but I'm still having a hard time understanding it despite having already read several forum threads and educational articles. Intuitively, the definition is stating that no matter how narrow we choose to make the "epsilon band"... -
E
Limit definition for derivation of f(x) HELPtutoring my daughter and I'm stuck
Homework Statement Here's the question...use the limit defintion to find the derivation of f(x) = x^2-4x Homework Equations does this use the defintion of the derivative formula (using Larson, et al 4th edition of Precaclulus graphing with limits...and trying to teach someone what to...- epatjn
- Thread
- Definition Derivation Limit Limit definition Stuck
- Replies: 2
- Forum: Precalculus Mathematics Homework Help
-
C
Limit definition of a derivative
Homework Statement I had my second exam last week for my Calculus I course. I did alright, but we are supposed to correct them and bring them back for a quiz grade. However, I wasn't sure how to do this one on the test, and did not magically figure it out since then :) Find the derivative...- crybllrd
- Thread
- Definition Derivative Limit Limit definition
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
T
Limit definition gives a contradiction
Limit definition gives a contradiction! say we are given sequences a(n), b(n) such that, a(n)->a, b(n)->b that means for epsilon>0, a-epsilon<a(n)<a+epsilon when n>N1 b-epsilon<b(n)<b+epsilon when n>N2 set N=max(N1,N2) when n>N...- torquerotates
- Thread
- Contradiction Definition Limit Limit definition
- Replies: 4
- Forum: Calculus
-
W
Find derivative of floor function using limit definition of derivative?
Homework Statement I have been asked to find the derivative of f(x) = 0.39 + 0.24*floor(x-1) using the limit definition of a derivative. Is this possible? Homework Equations The Attempt at a Solution The limit as h approaches zero of 0.24(floor(x+h-1)-floor(x-1))/h is as far as...- wills921
- Thread
- Definition Derivative Function Limit Limit definition
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-

Calculate Divergence using limit definition
Homework Statement Evaluate div v at P = (0, 0, 0) by actually evaluating (\int_S\mathbf{\hat{n}}\cdot \mathbf{v}\,dA)/V and taking the limit as B-->0. Take B to be the cube |x|\le\epsilon,|y|\le\epsilon,|z|\le\epsilon. Let \mathbf{v} = x\mathbf{\hat{i}} + 2y\mathbf{\hat{j}} -...- Saladsamurai
- Thread
- Definition Divergence Limit Limit definition
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
F
What is the Limit Definition for Proving a Function Approaches 0?
Hi. I'm a first-year calculus student and I'm fairly behind with my work. The transition is tough and when i read my textbook, I don't fully absorb everything. I thought I would post an example problem whose solution I do not follow completely, since it is fairly important in the scope of...- freshlikeuhh
- Thread
- Definition Limit Limit definition
- Replies: 1
- Forum: Calculus
-
R
Epsilon-delta proof of limit definition of e?
Homework Statement Prove that \lim_{x\rightarrow\ 0} (1+x)^{1/x}=e by an epsilon-delta proof. Homework Equations The Attempt at a Solution I did: x < a 1 + x < 1 + a but I couldn't go any further.- ryoma
- Thread
- Definition Limit Limit definition Proof
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
J
Finding a derivative from the limit definition
Homework Statement Find the derivative of f(x)=x1/3 using the limit definition of a derivative. Homework Equations The Attempt at a Solution I am stuck once I plug the numbers into the limit definition equation. How can I simplify the numerator in such a way the the h in the...- Jimmy25
- Thread
- Definition Derivative Limit Limit definition
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
C
Limit Definition of Derivative
Homework Statement Use the limit definition of derivative to determine the derivative of the following function: f(x) = { sqrt(x^2+1) if x<=0 0 if x>0 Homework Equations I'm not sure as to why the function is not continuous at x=0, and so it's not differentiable at that...- cjaylee
- Thread
- Definition Derivative Limit Limit definition
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
J
Use limit definition to prove
Ues the limit definition to prove that the stated limit is correct. \lim_{x->-2} \frac{1}{x+1}=-1. The limit def' is |f(x)-L|<epsilon if 0<|x-a|< delta. So we have |\frac{1}{x+1} + 1| < \epsilon if 0 < |x- (-2)| < \delta \mbox{ therefore } |\frac{1}{x+1}||x+2| < \epslion \mbox{ if } 0 < |x +...- John O' Meara
- Thread
- Definition Limit Limit definition
- Replies: 5
- Forum: General Math
-
S
Trying to fully grasp limit definition
Homework Statement An example in the text that involves showing that x^2sin\frac{1}{x} approaches 0 as x approaches 0.Homework Equations \epsilon -\delta argumentThe Attempt at a Solution I can prove many limits efficiently now using \epsilon -\delta but I don't think I am that flexible with...- snipez90
- Thread
- Definition Limit Limit definition
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
C
Derivative of 10^x using limit definition
Homework Statement Obtain the first derivative of 10x by the limit definition.Homework Equations f'(x)=limh->0 f(x+h)-f(x)/hThe Attempt at a Solution f'(x)=limh->0 10x+h-10x/h I also know that h=1 as x approaches 0. Now, how do I make it so that you aren't dividing by h=0.- cmajor47
- Thread
- Definition Derivative Limit Limit definition
- Replies: 16
- Forum: Calculus and Beyond Homework Help
-
P
Find Derivative of f(x)= 1/(2x-4) Using Limit Definition
Homework Statement Use the limit definition to find the derivative of the function. f(x)= 1/(2x-4) Homework Equations f(x+h)-f(x)/h The Attempt at a Solution ok so first i plugged it all in.. (1/(2(x+h)-4))-(1/(2x-4)) / h from here i was going to do fly-by with the two top...- Precal_Chris
- Thread
- Definition Limit Limit definition
- Replies: 22
- Forum: Precalculus Mathematics Homework Help
-
J
Using limit definition of multivariable derivative
Hi, everyone- I have a quick question. When you solve for the derivative (as a linear transformation) using the limit definition of derivative, how does it go? For example, let p_k be defined as the projection function from Rn to R, projecting onto kth coordinate of the input value... -
A
Proving Negation of Limit Definition
Homework Statement I'm trying to show that a sequence does not have a limit, so that would mean proving the negation of the limit definition is true, right? Is this a correct negation of the definition of what it means for a sequence to have a limit? Homework Equations The definition...- antiemptyv
- Thread
- Definition Limit Limit definition
- Replies: 3
- Forum: Calculus and Beyond Homework Help