Measure Definition and 1000 Threads
-
O
I Are slices of measurable functions measurable?
I decided to go through @psie's measure theory notes to refresh myself since it's been a while. I got to the theorem on page 60 which I will attempt to summarize my confusion as just this statement If X and Y are measure spaces and ##f:X\times Y\to \mathbb{C}## is measurable then the function...- Office_Shredder
- Thread
- Functions Measurable Measure
- Replies: 3
- Forum: Topology and Analysis
-

Basic infinitesmal doubt: Can there be a negative infinitesmal?
What I mean is on a coordinate plane like below we take the positive x axis measure a certain distance x on it and take the infinitesmally small quantity dx next to it in the positive direction: Now can I do the opposite as in can I measure a distance negative x on the negative x axis and...- tellmesomething
- Thread
- Measure Negative
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
S
I Measure of existence? (Stanford Encyclopedia of Philosophy)
I'm reading the article on the Many Worlds Interpretation in the Stanford Encyclopedia of Philosophy. I'm keeping up well, but this excerpt uses things I'm very unfamiliar with: I guess some characters weren't recognized. It's Section 3.6 here. I'm somewhat familiar with Wigner's Friend, but...- Sayestu
- Thread
- Existence Measure Quantum
- Replies: 7
- Forum: Quantum Interpretations and Foundations
-
W
A How to measure the two-photon detuning in 3-level system?
hi,everyone! if i have a 3-level system,like this: now,i want know how to measure the two-photon detuning in this system,and i‘ve known that,Δ2 and Δ3 are the two- and on-photon detunings,like this paper said: my questions are below: 1.how other researchers measure these two parameters? they...- wangvivi
- Thread
- Measure Quantum optics System
- Replies: 2
- Forum: Quantum Physics
-
C
B Is it possible to measure both position and momentum simultaneously?
A simultaneous measurement of both a particle's position and momentum may be successfully accomplished if more than one photon were utilized for the measurement. A non-demolishing measurement is possible if the emitters were aligned such that each would offset the other’s recoil of the target...- Clueless123
- Thread
- Measure Momentum Position
- Replies: 13
- Forum: Quantum Physics
-
L
Approaching the Measure of a Set: Strategies for Finding f(Eα)
my question is how can I approch the problem ? And what is explicitly the set f(Eα)? {f(x) ∈ [a, b] such that what ??}- laurabon
- Thread
- Measure Measure theory Real analysis Set
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
J
Best way to measure magnetic waves for electromagnetic induction
Hi all, Looking to measure some magnetic waves being generated at an electric coil. Freq is between 0-20kHz and magnitude is pretty small <1T. Any have suggestions for the best tool to measure and log data of this magnetic waveform? Googling around, I found meters like this: [Possible spam...- josh_TMS
- Thread
- Electromagnetic Electromagnetic induction Induction Magnetic Measure Waves
- Replies: 13
- Forum: Electrical Engineering
-

Insights How to Measure Internal Resistance of a Battery
Continue reading...- neilparker62
- Thread
- Battery Internal Internal resistance Measure Resistance
- Replies: 12
- Forum: Electromagnetism
-
S
How to measure solar panel voltage using arduino?
I would like to make the solar system a bit smarter. The challenge is that the voltage is high (up to 351Vdc) and the solar negative is typically 40-70V UNDER the "system ground". "System ground" is shared among battery negative, charger negative, inverter ground and ground cable digged down...- solvejskovlund
- Thread
- Arduino Measure Solar Solar panel Voltage
- Replies: 32
- Forum: Electrical Engineering
-

How do you measure time on a tide locked planet?
This is both a biomechanical and sociological question. There is a planet. It orbits around a large star whose goldilocks zone is significantly far from the star that the orbit is measured in thousands of Earth-years1. The planet is tide-locked2. The planet is otherwise the same size and...- AotrsCommander
- Thread
- Measure Planet Time
- Replies: 87
- Forum: Sci-Fi Writing and World Building
-
K
I Measuring Time & Spatial Distances: Timelike vs Spacelike
My book writes " The geometric distinction between timelike and spacelike distances is mirrored in the devices used to measure them. A clock is a device that measures timelike distances; a ruler is a device for measuring spacelike ones. Two nearby points or a timelike world line are timelike...- Kashmir
- Thread
- Clocks Mean Measure
- Replies: 11
- Forum: Special and General Relativity
-
K
I Using position of free particle to measure time
Hartle, Gravity "An observer in an inertial frame can discover a parameter ##t##with respect to which the positions of all free particles are changing at constant rates. This is time" Then goes on to say "Indeed, inertial frames could be defined as Cartesian reference frames for which Newton’s...- Kashmir
- Thread
- Free particle Measure Particle Position Time
- Replies: 18
- Forum: Special and General Relativity
-

MHB Outer measure .... Axler, Result 2.8 ....
I am reading Sheldon Axler's book: Measure, Integration & Real Analysis ... and I am focused on Chapter 2: Measures ... I need help with the proof of Result 2.8 ... Result 2.8 and its proof read as follows In the above text from Axler we read:"The doubly indexed collection of open...- Math Amateur
- Thread
- Measure
- Replies: 2
- Forum: Topology and Analysis
-
E
Chemistry How to measure the density of a material?
ohh- EL AALLAOUI Najla
- Thread
- Density Material Measure
- Replies: 9
- Forum: Biology and Chemistry Homework Help
-

I Will the upcoming experiment PICO measure kSZ temperature anisotropy?
I know for sure PICO will be measuring polarization anisotropies with high fidelity. In addition, the PICO science paper shows that it will make full-sky Compton-y maps but the plots are mostly limited to l=1000. Will PICO be able to measure kSZ temperature anisotropy at l=3000?- SherLOCKed
- Thread
- Cmb Cosmology Experiment Measure Temperature Upcoming
- Replies: 1
- Forum: Cosmology
-
I How to Measure Speed of Light & Is It Constant?
The question constantly arises how the speed of light is measured and what does it mean that the speed is constant, including at remote points for the observer, including at points beyond the local frame of reference, as you understand it in general relativity (GR). First of all, it should be...- mef
- Thread
- Constant Light Measure Schwarzschild metric Speed Speed of light
- Replies: 13
- Forum: Special and General Relativity
-
R
A Measure of non-periodicity of almost periodic functions
As is well known, almost periodic functions can be represented as a Fourier series with incommensurable (non-multiple) frequencies https://en.wikipedia.org/wiki/Almost_periodic_function. It seems to me that I came up with an integral criterion for the degree of non-periodicity. The integral of a...- reterty
- Thread
- Functions Measure Periodic Periodic functions
- Replies: 1
- Forum: General Math
-
J
Entropy: Does Disorder Really Measure Order?
Let's say you have a very dirty small room room and a giant clean library (lots of organized books) and let's say these occupy the same number of microstates. The entropy according to this equation is the same for the library and the room. But one is more ordered than the other one. How does it...- Jaccobtw
- Thread
- Disorder Entropy Measure
- Replies: 8
- Forum: Introductory Physics Homework Help
-

MHB Finding the Measure of Angle KPM Using Angle Bisector Theorem
Ray $\overline{PK}$ bisects and the measure of $\angle{LPM}$ is $11x^o$ and the measure of $\angle{LPK}$ is $(4x+18)^o$ What is the measure of $\angle{KPM}$ $s.\ 12^o \quad b.\ 28\dfrac{2}{7}^o \quad c. \ 42^o \quad d. \ 61\dfrac{1}{5}^o \quad e. \ 66^o$- karush
- Thread
- Angle Measure
- Replies: 2
- Forum: General Math
-
P
I Standard measure of distance from equilibrium for all systems
Is there a standard way to measure how far a system is displaced from equilibrium that can be applied to all physical systems? So, for example, a ball that is kicked, a spring that is stretched, a liquid that’s heated, and a charged battery are all systems that are displaced from equilibrium. I...- pepperellrob
- Thread
- Equilibrium Equilibrium of forces Measure Nonequilibrium Standard Systems
- Replies: 2
- Forum: Thermodynamics
-
G
Special relativity - measure of a rod and simultaneity
Hi, I´m trying to solve a special relativity problem, and I think I need some help. There are two inertial frames of reference, ##O## and ##O'##, the last one moving with relative velocity ##v## in the ##x## direction. There's a rod with length ##L'## fixed to frame ##O'##, such that front end...- Gom
- Thread
- Lorentz transformations Measure Relativity Rod Simultaneity Special relativity
- Replies: 2
- Forum: Introductory Physics Homework Help
-
V
I How can we observe and measure interacting vacuum?
When studying the QFT, one considers the vacuum state when the field is not excited and therefore no particles are present. Now for the matter fields this makes sense to me. But what about the radiation field? Suppose we have an arbitrary small volume of space in the universe without any matter...- victorvmotti
- Thread
- Measure Vacuum
- Replies: 1
- Forum: Quantum Physics
-
S
B What is dTau? The Role of dTau in Measuring Time on a Worldline
I heard dTau measures time for the person traveling on a worldline. If the person traveling on that world line chalked marks on the world line every 1 minute, would those intervals be the same distance from each other?- sqljunkey
- Thread
- Measure
- Replies: 3
- Forum: Special and General Relativity
-
M
B Measuring Light Velocity Correctly: Thought Experiment
Let there be a track 450,000 km long and a rocket 300,000 km long with a laser attached to the bottom of it's back end with a clock beside it, and a second synchronized clock attached to bottom of its front end. Both clocks were also synchronized with a track clock while the rocket was parked...- Magatron
- Thread
- Experiment Light Light speed Lorentz transformation Measure Thought experiment Velocity
- Replies: 28
- Forum: Special and General Relativity
-

B Observers sending signals to measure expansion
Googling you find a current expansion rate of ~70 km/s or 0.0002C but of course we don't observe this with objects in the solar system as local gravity prevents this expansion - otherwise a distances would increase by a light second roughly every 71 minutes (maybe I’m missing some here... -

I Can you practically measure an infinite amount of some quantity?
Suppose we measure some speed or energy of something with a suitable device or instrument. Now suppose the quantity that is being measured exceeds the capabalities of the measuring device either from above or below. How can we know if this quantity is indeed finite and not infinite?- MathematicalPhysicist
- Thread
- Infinite Measure
- Replies: 10
- Forum: Other Physics Topics
-
B
How to Measure and Display Rapidly Varying Vertical Forces from a Rotating Mass?
how do I measure a rapidly and cyclically varying vertical force I have a rotating mass that generates centrifugal and aerodynamic forces. I want to see the variation thru one rotation at steady state. how do I measure the vertical force generated and display it on my computer screen, with a...- Bob Higgins
- Thread
- Force Measure
- Replies: 22
- Forum: Mechanical Engineering
-

B Can we measure acceleration of galaxies and stars?
As for example we see a large void, the Great Repeller, which in fact is an underdense region, and with respect to this region, matter seems to be repelled by this region. The explenation for that is that matter outside that regions pulls on the matter inside it. But if that is really the... -
C
A Effects of a spatially nonuniform diffusion parameter
Einstein famously derived his relation between the diffusion constant of Brownian motion, particle mobility in a disippative medium, and temperature by considering Brownian motion in a harmonic oscillator potential. The result, $D = \mu k_BT$, is derived assuming that the mobility $\mu$ is...- Couchyam
- Thread
- Diffusion Effects Measure Parameter Statistical mechanics
- Replies: 6
- Forum: Other Physics Topics
-
F
MHB Proving Measure Space Properties of $(X,\bar{\mathcal{B}} ,\bar{\mu})$
Hello, I have problems with this exercise Let $(X,\mathcal{B} , \mu)$ a measurement space, consider $\bar{\mathcal{B}} = \{ A \subseteq{X} \; : \; A\cap{B} \in \mathcal{B}$ for all that satisfies $\mu(B) < \infty \}$, and for $A \in \bar{\mathcal{B}}$ define $\bar{\mu}(A) = \left \{...- fabiancillo
- Thread
- Measure Properties Space
- Replies: 2
- Forum: Topology and Analysis
-
K
I How to measure a 10 Hz energy splitting of two energy levels
Hello! If I have 2 energy levels split by something of the order of 10 Hz (they can be connected by an electric dipole moment i.e. ##\Delta J = 0## and they have different parities), what would be the best way to measure this difference (even 10% error would be good, but the lower the error the...- kelly0303
- Thread
- Energy Energy levels Levels Measure Splitting
- Replies: 29
- Forum: Atomic and Condensed Matter
-

How to Measure Very Small Differential Pressure in a Subsonic Wind Tunnel
I assume that air have ##1 kg/m^3## density. Therefore, using Bernoulli equation, on upside and downside of my test object, there is a differential pressure ##\Delta P##: $$\Delta P=0.5*(v_2^2 - v_1^2)$$ From cases: (a) ##v_1 = 1 m/s## and ##v_2 = 2 m/s##, then ##\Delta P = 1,5 Pa## (b) ##v_1 =...- agnimusayoti
- Thread
- Differential Measure Pressure Wind Wind tunnel
- Replies: 29
- Forum: Mechanical Engineering
-
K
I Smallest energy we can measure
Hello! Assuming we can bring 2 energy levels very close to each other (e.g. by applying a magnetic field), what is the practical limit (in terms of lab equipment) on the smallest energy difference that we can measure? And what is the relative error on it, that can be obtained? For example if the...- kelly0303
- Thread
- Energy Measure
- Replies: 13
- Forum: Atomic and Condensed Matter
-
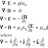
Measure angular velocity and acceleration from missing tooth wheel
Hi, I need to come up with a math model for a digital ignition system. I've been thinking about it and I think that I need to measure 2 things to be able to calculate when I have to start charging the coil. They are the angular velocity and the acceleration but how can I do it? the idea is to... -
A
Analysis Prerequisites Measure theory for ug student in physics
Hi, I would like to know if an undergraduate student in physics could be able to study measure theory in order to have a better understanding of the probability theory and go further in this way (stochastic process) ? Assuming a first year of calculus and the level of "Mathematical methods in...- azeow
- Thread
- Measure Measure theory Physics Prerequisites Student Theory
- Replies: 11
- Forum: Science and Math Textbooks
-
A
Why does the top surface of a Silicon Die measure close to 0 ohms?
I have gotten access to a large bare silicon die (almost 1" across, 14nm process) that my company gets from a fab. I've been monkeying around with an ohmmeter placed at the top of the die, with the test leads placed at various points around the die, and I almost always measure the same value...- austinuni
- Thread
- Measure Ohms Silicon Surface
- Replies: 5
- Forum: Electrical Engineering
-
S
I To measure a Planck length would require a black-hole photon?
I was viewing this video in which the narrator says that the energy of a photon that could discern a Planck length would require a photon of such high energy that it would be a de factor black hole. Is this accurate?- swampwiz
- Thread
- Length Measure Photon Planck Planck length
- Replies: 10
- Forum: Quantum Physics
-
S
How to Measure Torque Required for motor to spin a rotating shaft?
I've harvested a motor from a cordless drill and connected it to a belt which turns a rotating shaft. The motor pulley and the pulley on the other side of the belt are roughly the same size, which a fairly small radius (5 mm maybe?). The issue I'm running into, which I don't fully understand...- Scott 33
- Thread
- Measure Motor Rotating Shaft Spin Torque
- Replies: 3
- Forum: Mechanical Engineering
-

B Length is the measure of intervals in space?
What does 'intervals' mean here?- sahilmm15
- Thread
- intervals Length Measure Space
- Replies: 11
- Forum: Classical Physics
-

Measure Planck's constant without universal constants
I am not getting any ideas to solve this without the universal constants. The method that I want to use invloves the speed of light, which is a universal constant.- Heisenberg_white
- Thread
- Constant Constants Measure Universal
- Replies: 3
- Forum: Advanced Physics Homework Help
-
K
I Is it feasible to measure one way speed of light this way?
Theoretical experiment for measuring one way speed of light From 1905 to this day we have not experimentally measured the one way speed of light between a source to the detector only the roundtrip from the source to the detector and back again. We just assume that the speed of light is the...- kostarak
- Thread
- Light Measure Speed Speed of light
- Replies: 52
- Forum: Special and General Relativity
-

Measure the distance to a star using magnitude and extinction
Hello, I'm struggling with this question A star is observed close to the center of the Milky Way and from its spectrum we find that it is a type A3 star. Its observed magnitude is m_v = 25. There is only a diffusive gas between us and the star, so we can assume an extinction, of 1 magnitude per...- Mikkel
- Thread
- Astrophysics Extinction Magnitude Measure Star
- Replies: 8
- Forum: Introductory Physics Homework Help
-

I A claim in measure theory which seems flawed to me
The claim states the following: Let ##(X,\mathcal{A},\mu)## be a measurable space, ##E## is a measurable subset of ##X## and ##f## is a measurable bounded function which has a bounded support in ##E##. Prove that: if ##f\ge 0## almost everywhere in ##E##, then for each measurable subset...- MathematicalPhysicist
- Thread
- Measure Measure theory Theory
- Replies: 15
- Forum: Set Theory, Logic, Probability, Statistics
-

How did Tesla measure electromagnetic fields, etc?
He didn’t have the modern equipment we have today.- Macoleco
- Thread
- Electromagnetic Electromagnetic fields Fields Measure Tesla
- Replies: 3
- Forum: Electrical Engineering
-

B Radian measure and real numbers
Formula used : arc length = radius × angle (in radian). I interpreted this as: •Taking a unit circle, we get "angle (in radian) = arc length". This means radian measure of an angle is arc length, which can be represented on a real number line. Hence, it is a real number. Is this way to...- f9CSERS
- Thread
- Measure Numbers Real numbers
- Replies: 9
- Forum: General Math
-
T
How to Measure and Calculate Band Gap of a Photovoltaic Device
Hi there! I bought a photovoltaic cell. I would like to learn its band gap at 300 K and 0 K. How can i measure band gap or calculate? I have already measured Temperature to Vmax values. I couldn't find any good information about this topic. Thanks.- tornado
- Thread
- Band Band gap Device Gap Measure Photovoltaic
- Replies: 3
- Forum: Electrical Engineering
-
H
A How can we measure these Hermitian operators?
Hi Pf, I am reading this article about generalization of Pauli matrices https://en.wikipedia.org/wiki/Generalizations_of_Pauli_matrices#Generalized_Gell-Mann_matrices_%28Hermitian%29 When i receive a qubit in a given density matrix , i can measure the mean values of the Pauli matrices by...- Heidi
- Thread
- Hermitian Measure Operators
- Replies: 9
- Forum: Quantum Physics
-
A
B How can we measure the wavelength of gamma-rays?
How can we experimentally measure the wavelength of gamma-rays, say for about 0.7MeV? Can it be done without gamma-ray spectrometry?- avicenna
- Thread
- Measure Wavelength
- Replies: 10
- Forum: High Energy, Nuclear, Particle Physics
-
J
How to Measure PCB Impedance and Component Coupling?
I am designing a PCB with multiple capacitors on it. I would like to measure the board impedance to compare it with results from Ansys Q3D. I can connect it to an impedance analyzer and easily get the impedance. I have recently thought about other meaningful measurements that I may be able to...- js2020
- Thread
- Component Coupling Impedance Measure Pcb
- Replies: 12
- Forum: Electrical Engineering
-

Best way to measure non-thermal expansion of a pipe
Ideally, the method should be accurate down to 0.01 millimetres or better. We're probably talking pipes of up to 150 mm (6") diameter. Accurately measuring the actual diameter of the pipe is of less importance - it's how much it expands that matters. My idea is wrapping something around the...- Jehannum
- Thread
- Expansion Measure Pipe
- Replies: 6
- Forum: Mechanical Engineering