Partial derivative Definition and 363 Threads
-
W
I Partial derivative of Dirac delta of a composite argument
I'm trying to prove the following statement: $$ D\partial_t\left(\delta\circ\mathbf{v}\right) = J^i\partial_i\left(\delta\circ\mathbf{v}\right), $$ where ##\mathbf{v}## is some function of time and ##n##-dimensional space, ## D ## is the Jacobian determinant associated with ##\mathbf{v}##, that...- William Crawford
- Thread
- Composite function Dirac delta Partial derivative
- Replies: 2
- Forum: Calculus
-
L
I Differentiability of a Multivariable function
I’m having a little confusion about part b of this question as to why I am allowed to use the limit definition of a partial derivative. Here’s what I think: I know that y^3/(x^2+y^2) is undefined at the origin but it does approach 0 when it GETS CLOSE to the origin. So technically defining... -

Need a real life example where a partial derivative is used in motion
my group is preferring the ue of partial derivative to find the acceleration of a car or the projectile motion of something being launched- nrsakinh
- Thread
- Motion Partial derivative
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

Potential in the three regions of an infinite slab
for the boundary conditions for this problem I understand that Electric field and Electric potential will be continuous on the boundaries. I also know that I can set the reference point for Electric potential, wherever it is convenient. This gives me the fifth boundary condition. I am confused...- workhorse123
- Thread
- Boundary condition Laplace equation Partial derivative
- Replies: 1
- Forum: Advanced Physics Homework Help
-
S
Find f(x,y) given partial derivative and initial condition
My attempt: $$\frac{\partial f}{\partial x}=-\sin y + \frac{1}{1-xy}$$ $$\int \partial f=\int (-\sin y+\frac{1}{1-xy})\partial x$$ $$f=-x~\sin y-\frac{1}{y} \ln |1-xy|+c$$ Using ##f(0, y)=2 \sin y + y^3##: $$c=2 \sin y + y^3$$ So: $$f(x,y)=-x~\sin y-\frac{1}{y} \ln |1-xy|+2 \sin y + y^3$$ Is...- songoku
- Thread
- Calculus Partial derivative
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
B
Partial Derivative Simplification
Hi there! I would like to know if the following simplification is correct or not: Let A be a function of x, y, and z $$\frac{\partial^2A}{\partial x^2}+\frac{\partial^2A}{\partial y^2}$$ $$=\ \frac{\partial^2A\partial y^2+\partial^2A\partial x^2}{\partial x^2\partial y^2}$$...- BlackMelon
- Thread
- Function Partial derivative
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
S
Multivariable calculus problem involving partial derivatives along a surface
I just wanted to know if my solution to part (b) is correct. Here's what I did: I took the partial derivative with respect to x and y, which gave me respectively. Then I computed the partial derivatives at (-3,4) which gave me 3/125 for partial derivative wrt x and -4/125 for partial derivative...- sss1
- Thread
- Calculus Multivariable Partial derivative
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-

Find the partial diameter error of the surface area of cylinder
(ΔSA/ΔD) = 2πHΔD Something is wrong I guess as I get wrong value.- abobik
- Thread
- Cylinder Derivative Partial derivative Surface area
- Replies: 3
- Forum: Introductory Physics Homework Help
-
M
Find Isobaric Expansion & Pressure-Volume Coefficient for Solid
The answer to this problem is However, I am confused how this relates to the question. My working is, ##V = cT^2 - bpT## ##\frac{dV}{dT} = 2cT - bp## (I take the partial derivative of volume with respect to temperature to get the isobaric expansion coefficient) ##\frac{dV}{dP} = 0## (I take...- member 731016
- Thread
- Equation of state Partial derivative
- Replies: 4
- Forum: Introductory Physics Homework Help
-

For this Partial Derivative -- Why are different results obtained?
Given a function F(x,y)=A*x*x*y, calculate dF(x,y)/d(1/x), to calculate this derivative I make a change of variable, let u=1/x, then the function becomes F(u,y)=A*(1/u*u)*y, calculating the derivative with respect to u, we have dF/du=-2*A*y*(1/(u*u *u)) replacing we have dF/d(1/x)=-2*A*x*x*x*y...- Silvia2023
- Thread
- Calculus Function Partial derivative
- Replies: 26
- Forum: Calculus and Beyond Homework Help
-
P
What does this expression involving Partial Derivatives mean?
I already solved w x x/|x| For (w1,w2,w3) and (x1,x2,x3)- physicss
- Thread
- Derivation Partial derivative
- Replies: 5
- Forum: Introductory Physics Homework Help
-

I Finding the time for the first shock for a quasilinear first order PDE
To find a shock wave, do we always solve the equation ##x_{\xi}=0##? The PDEs I consider are of the form ##u_t + g(u) u_x = f(u)##, with initial condition ##u(x,0) = h(x)##. I have been looking at the solutions for problems in my homework sheet but this method was used with no explanation. Why...- BloonAinte
- Thread
- Partial derivative Partial differential equations
- Replies: 4
- Forum: Differential Equations
-
N
Correct Usage of Partial Derivative Symbols in PDEs
Some may say that ##\frac{ \partial g }{ \partial t }## is correct because it is a term in a partial differential equation, but since ##g## is a one variable function with ##t## only, I think ##\frac{ dg }{ dt }## is correct according to the original usage of the derivative and partial...- nizi
- Thread
- Derivative Partial Partial derivative Partial derivatives Partial differential equations Pdes Symbols
- Replies: 10
- Forum: Calculus and Beyond Homework Help
-
L
B Question about the definition of a partial derivative
I just started to study thermodynamics and very often I see formulas like this: $$ \left( \frac {\partial V} {\partial T} \right)_P $$ explanation of this formula is something similar to: partial derivative of ##V## with respect to ##T## while ##P## is constant. But as far as I remember...- lerus
- Thread
- Definition Derivative Partial Partial derivative
- Replies: 13
- Forum: Thermodynamics
-
G
I Understanding Covariant and Partial Derivatives in General Relativity
In the 128 pages of 《A First Course in General Relativity - 2nd Edition》:"The covariant derivative differs from the partial derivative with respect to the coordinates only because the basis vectors change."Could someone give me some examples?I don't quite understand it.Tanks!- GR191511
- Thread
- Covariant Covariant derivative Derivative Partial Partial derivative
- Replies: 5
- Forum: Special and General Relativity
-
J
Calculating the partial derivative in polar coordinates
Hello, I am trying to solve the following problem: If ##z=f(x,y)##, where ##x=rcos\theta## and ##y=rsin\theta##, find ##\frac {\partial z} {\partial r}## and ##\frac {\partial z} {\partial \theta}## and show that ##\left( \frac {\partial z} {\partial x}\right){^2}+\left( \frac {\partial z}...- james weaver
- Thread
- Coordinates Derivative Partial Partial derivative Polar Polar coordinates
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-

I From a proof on directional derivatives
Given that the partial derivatives of a function ##f(x,y)## exist and are continuous, how can we prove that the following limit $$\lim_{h\to 0}\frac{f(x+hv_x,y+hv_y)-f(x,y+hv_y)}{h}=v_x\frac{\partial f}{\partial x}(x,y)$$ I can understand why the factor ##v_x## (which is viewed as a constant )... -
J
I Partial Derivative of Convolution
Hello, I am trying to calculate the partial derivative of a convolution. This is the expression: ##\frac{\partial}{\partial r}(x(t) * y(t, r))## Only y in the convolution depends on r. I know this identity below for taking the derivative of a convolution with both of the functions only... -
A
Calculating specific heat capacity from entropy
Hey guys! I'm currently struggling with a specific thermodynamics problem. I'm given the entropy of a system (where ##A## is a constant with fitting physical units): $$S(U,V,N)=A(UVN)^{1/3}$$I'm asked to calculate the specific heat capacity at constant pressure ##C_p## and at constant volume...- approx12
- Thread
- Capacity Entropy Heat Heat capacity Partial derivative Specific Specific heat Specific heat capacity Thermodyamics
- Replies: 1
- Forum: Advanced Physics Homework Help
-
L
A Heisenberg equation of motion -- Partial derivative question
Heisenberg equation of motion for operators are given by i\hbar\frac{d\hat{A}}{dt}=i\hbar\frac{\partial \hat{A}}{\partial t}+[\hat{A},\hat{H}]. Almost always ##\frac{\partial \hat{A}}{\partial t}=0##. When that is not the case?- LagrangeEuler
- Thread
- Derivative Equation of motion Heisenberg Motion Partial Partial derivative
- Replies: 15
- Forum: Quantum Physics
-
S
A Index notation and partial derivative
Hi all, I am having some problems expanding an equation with index notation. The equation is the following: $$\frac {\partial{u_i}} {dx_j}\frac {\partial{u_i}} {dx_j} $$ I considering if summation index is done over i=1,2,3 and then over j=1,2,3 or ifit does not apply. Any hint on this would... -
D
Help taking a partial derivative
Hi all, I was wondering is if the following partial derivative can be computed without a specific ##u(t,x)## $$\partial_tu\big[(t,x-t\kappa V)\big]$$ I was thinking it can't be done, because we could have $$u_a(t,x)=tx \Rightarrow \partial_tu\big[(t,x-t\kappa...- docnet
- Thread
- Derivative Partial Partial derivative
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
J
Solving a Partial Derivative Problem Step-by-Step
So I start by isolating v the speed here would be the square root of the partial t derivative divided by the sum of the partial x and y derivatives. the amplitude, phi and the cos portion of the partial derivatives would all cancel out. What I am left with is the sqrt(43.1 / ( 2.5 + 3.7 ) =...- JoeyBob
- Thread
- Derivative Partial Partial derivative
- Replies: 5
- Forum: Introductory Physics Homework Help
-
F
I Divergence & Curl -- Is multiplication by a partial derivative operator allowed?
Divergence & curl are written as the dot/cross product of a gradient. If we take the dot product or cross product of a gradient, we have to multiply a function by a partial derivative operator. is multiplication by a partial derivative operator allowed? Or is this just an abuse of notation -
P
Interpreting a thermodynamics formula using a picture
I notice that ##pv=t## looks like the ideal gas law but with ##T## in units of energy. I know that ##pV = \text{constant}## means that the pressure of a gas decreases as you expand it (Boyle-Mariotte's law), explaining for instance how we breathe. I guess I could put everything in words even...- PhysicsKush
- Thread
- Formula Partial derivative Picture Thermodynamics
- Replies: 11
- Forum: Advanced Physics Homework Help
-
R
I Why Does the Partial Derivative of a Sum Cancel Out?
Why the summation of the following function will be canceled out when we take the partial derivative with respect to the x_i? Notice that x_i is the sub of (i), which is the same lower limit of the summation! Can someone, please explain in details? -
M
Partial derivative of Vxx w.r.t. r in terms of Vxx
Can anyone please help me to write partial derivative of Vxx w.r.t. r in terms of Vxx as shown in the hand written box at the end.- mramzan476
- Thread
- Derivative Partial Partial derivative Terms
- Replies: 2
- Forum: Calculus
-

Sign of a second partial derivative
I am not sure how to determine the sign of this derivatives. (a) first we can pass a plane by (1,2) parallel to XZ (y fixed) and see how the curve belongs to the plane will vary with x, but what about the next partial derivative, with respect to y?- LCSphysicist
- Thread
- Derivative Partial Partial derivative Sign
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
S
B Reconciling basis vector operators with partial derivative operators
Ref. 'Core Principles of Special and General Relativity' by Luscombe. Apologies in advance for the super-long question, but it's necessary to show my thought process. Let ##\gamma:I\to M## be a smooth curve from an open interval ##I\subset\mathbb{R}## to a manifold ##M##, and let...- Shirish
- Thread
- Basis Derivative Operators Partial Partial derivative Vector
- Replies: 4
- Forum: Differential Geometry
-

Improving vertical symbol spacing in partial derivative equations
It's a detail, but annoying to me: ##{\partial u\over \partial x} = {\partial \phi \over \partial x} \;+ ...## $${\partial u\over \partial x} = {\partial \phi \over \partial x} \;+ ...$$ How do I move up ##\partial u## a little bit so it aligns with ##\partial \phi## ?- BvU
- Thread
- Derivative Partial Partial derivative Symbol Vertical
- Replies: 1
- Forum: MATLAB, Maple, Mathematica, LaTeX
-
R
Can we take the partial derivatives of φ and ψ here?
I research about coordinate systems and I found the following informations about transformation. Now, if I replace arctan (x/y) (according to the picture above) to φ, I think I can solve. But if I can do this, then what will be replaced to ψ? I mean, I know just taking partial derative about...- requied
- Thread
- Derivatives Partial Partial derivative Partial derivatives
- Replies: 22
- Forum: Calculus and Beyond Homework Help
-
A
I The Ratio of Total Derivatives
If we have two functions C(y(t), r(t)) and I(y(t), r(t)) can we write $$\frac{\frac{dC}{dt}}{\frac{dI}{dt}}=\frac{dC}{dI}$$?- Ahmed Mehedi
- Thread
- Calculus Derivatives Differentiation General math Partial derivative Ratio
- Replies: 3
- Forum: General Math
-
A
I Understanding Mixed Partial Derivatives: How Do You Solve Them?
While working at home during the COVID-19 pandemic I've taken to seeing if I can still do math from undergrad (something I do once in a while to at least pretend my life isn't dominated by excel). So to that I've been reviewing partial derivatives (which I haven't really thought about in a good...- atomicpedals
- Thread
- Derivative Partial Partial derivative
- Replies: 3
- Forum: Calculus
-

A Partial derivative of composition
Hi guys, suppose we have a function ##C(x, y)## into the real numbers. Suppose also that ##y=y(x)##, i.e. ##y## is a function of ##x##. Now in my script, I have a term ##\nabla_x C(x_0, y(x_0)) ##. From my point of view, this means that you take the partial derivative of ##C(x,y)## with...- SchroedingersLion
- Thread
- Composition Derivative Partial Partial derivative
- Replies: 6
- Forum: General Math
-

Negative or Positive Partial Derivative
My attempt I calculated the partial derivatives of n wrt P and T. They are given below. ##\frac {\partial n}{\partial P} = \frac{nb -1}{\left(2an-Pb-3abn^2-kT\right )}## ##\frac {\partial n}{\partial T}= \frac {nk}{\left(2an-Pb-3abn^2-kT \right ) }## I know that if the partial derivative is...- Saptarshi Sarkar
- Thread
- Derivative Negative Partial Partial derivative Positive
- Replies: 2
- Forum: Advanced Physics Homework Help
-

Partial Derivative of a formula based on the height of a cylinder
The function should use (r,z,t) variables The domain is (0,H) Since U is not dependent on angle, then theta can be ignored in the expression for Laplacian in cylindrical coordinates(?)- currently
- Thread
- Cylinder Derivative Formula Height Partial Partial derivative Partial differential equations
- Replies: 1
- Forum: Advanced Physics Homework Help
-

Triple Product Rule Equivalency
##p=\frac {RT} v;~p=p(T,v)~...1## ##v=\frac {RT} p;~v=v(T,p)~...2## ##T=\frac {pv} R;~T=T(p,v)~...3## ##Considering~eq.~1:## ##p=\frac {RT} v \Rightarrow (\frac {\partial p} {\partial v})_T=-\frac {RT} {v^2}## ##Considering~eq.~2:## ##v=\frac {RT} p \Rightarrow (\frac {\partial v}...- WhiteWolf98
- Thread
- Ideal gas law Partial derivative Product Product rule
- Replies: 2
- Forum: Introductory Physics Homework Help
-

I Question about a partial derivative
I apologise for the length of this question. It is probably possible to answer it by reading the first few lines. I fear I have made a childish error: I am working on the geodesic equation for the surface of a sphere. While doing so I come across the partial derivative \begin{align}...- George Keeling
- Thread
- Derivative Geodesic Partial Partial derivative Partial derivatives Sphere
- Replies: 7
- Forum: Differential Geometry
-
C
Differential Integration Problem
Attempt at solution: Writing the chain rule for ## E(V,T) ##: ## dE = \frac{\partial E}{\partial T}dT + \frac{\partial E}{\partial V}dV ## Then, integrating the differential: ## \int{ dE } = \int{ \frac{\partial E}{\partial T}dT } + \int{ \frac{\partial E}{\partial V}dV } ## If I put the...- CGandC
- Thread
- Differential Integral Integration Partial derivative
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
F
A The partial derivative of a function that includes step functions
I have this function, and I want to take the derivative. It includes a unit step function where the input changes with time. I am having a hard time taking the derivative because the derivative of the unit step is infinity. Can anyone help me? ##S(t) = \sum_{j=1}^N I(R_j(t)) a_j\\ I(R_j) =... -
A
I Partial Derivative: Correct Formulation?
If given a function ##u(x,y) v(x,y)## then is it correct to write ##\frac{\partial }{\partial x}u(x,y)v(x,y)=\frac{u(x+dx,y)v(x+dx,y)-u(x,y)v(x,y)}{dx}##??- Apashanka
- Thread
- Derivative Partial Partial derivative
- Replies: 6
- Forum: General Math
-
A
Finding the partial derivative from the given information
It seems that the way to combine the information given is z = f ( g ( (3r^3 - s^2), (re^s) ) ) we know that the multi-variable chain rule is (dz/dr) = (dz/dx)* dx/dr + (dz/dy)*dy/dr and (dz/ds) = (dz/dx)* dx/ds + (dz/dy)*dy/ds ---(Parentheses indicate partial derivative) other perhaps...- Amadeo
- Thread
- Derivative Information Partial Partial derivative
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-

I Partial derivative interpretation
How do I interpret geometrically the partial derivative in respect to a constant of a function such as ##\frac{ \partial}{\partial c} (acos(x) + be^x + c)^2##? -
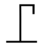
Help explaining the chain rule please
I had already calculated the first partial derivative to equal the following: $$\frac{\partial y}{\partial t} = \frac{\partial v}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial v}{\partial t}$$ Now the second partial derivative I can use the chain rule to do and get to...- Boltzman Oscillation
- Thread
- Calculus 2 Chain Chain rule Partial derivative
- Replies: 12
- Forum: Calculus and Beyond Homework Help
-

A Multi-variable function depending on the Heaviside function
How can I calculate ∂/∂t(∫01 f(x,t,H(x-t)*a)dt), where a is a constant, H(x) is the Heaviside step function, and f is I know it must have something to do with distributions and the derivative of the Heaviside function which is ∂/∂t(H(t))=δ(x)... but I don't understand how can I work with the... -
K
Meaning of subscript in partial derivative notation
Homework Statement I'm given a gas equation, ##PV = -RT e^{x/VRT}##, where ##x## and ##R## are constants. I'm told to find ##\Big(\frac{\partial P}{\partial V}\Big)_T##. I'm not sure what that subscript ##T## means? Homework Equations ##PV = -RT e^{x/VRT}## Thanks a lot in advance.- kaashmonee
- Thread
- Derivative Notation Partial Partial derivative
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
D
Derivative for a Galilean Tranformation
Homework Statement Using the chain rule, find a, b, c, and d: $$\frac{\partial}{\partial x'} = a\frac{\partial}{\partial x} + b\frac{\partial}{\partial t}$$ $$\frac{\partial}{\partial t'} = c\frac{\partial}{\partial x} + d\frac{\partial}{\partial t}$$ Homework Equations Chain rule...- doggydan42
- Thread
- Chain rule Derivative Galilean Galilean transformation Partial derivative
- Replies: 5
- Forum: Advanced Physics Homework Help
-

Solving Second Order Partial Derivative By Changing Variable
1. The problem statement, all variables, and given/known data Given is a second order partial differential equation $$u_{xx} + 2u_{xy} + u_{yy}=0$$ which should be solved with change of variables, namely ##t = x## and ##z = x-y##. Homework Equations Chain rule $$\frac{dz}{dx} = \frac{dz}{dy}...- Peter Alexander
- Thread
- Chain rule Change of variables Derivative Partial Partial derivative Partial differential equations Partial differentiation Second order Variable
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-

Is D(x,t) = ln(ax+bt) a solution to the wave function?
Homework Statement Show that the displacement D(x,t) = ln(ax+bt), where a and b are constants, is a solution to the wave function. Homework Equations I'm not sure which one to use: D(x,t) = Asin(kx+ωt+φ) ∂2D/∂t2 = v2⋅∂2D/∂x2 The Attempt at a Solution I'm completely lost on where to start...- Jamie_Pi
- Thread
- Function Partial derivative Wave Wave function
- Replies: 9
- Forum: Introductory Physics Homework Help
-
C
Partial derivative w.r.t. another partial derivative
Homework Statement Given $$L = \left(\nabla\phi + \dot{\textbf{A}}\right)^2 ,$$ how do you calculate $$\frac{\partial}{\partial x}\left(\frac{\partial L}{\partial(\partial\phi / \partial x)}\right)?$$ Homework Equations By summing over the x, y, and z derivatives, the answer is supposed to...- cc94
- Thread
- Derivative Partial Partial derivative
- Replies: 2
- Forum: Advanced Physics Homework Help