Volume integral Definition and 48 Threads
-
P
I Change of Variables in Double Volume Integral
In Greiner's Classical Electromagnetism book (page 126) he has a derivation equivalent to the following. $$\int_V d^3r^{'} \nabla \int_V d^3r^{''}\frac {f(\bf r^{''})}{|\bf r + \bf r^{'}- \bf r^{''}|}$$ $$ \bf z = \bf r^{''} - \bf r^{'} $$ $$\int_V d^3r^{'} \nabla \int_V d^3z \frac {f(\bf z +... -
D
Volume integral of x^2 + (y-2)^2 +z^2 = 4 where x , y , z > 0
(a) i sketched a quarter of a sphere centred at x=0 , y=2 , z=0 (b ) ∫ ∫ √ (4-x2 - (y-2)2) dx dy with limits 0 < x < 2 and 0 < y <4 (c ) i converted to spherical polars and took the integrand as 1/r2 . the volume element is r2sinθ drdθd∅ This leads to the triple integral of sinθ with...- dyn
- Thread
- Integral Volume Volume integral
- Replies: 21
- Forum: Calculus and Beyond Homework Help
-

Volume integral over a gradient (quantum mechanics)
Homework Statement 1) Calculate the density of states for a free particle in a three dimensional box of linear size L. 2) Show that ##\int f \nabla g \, d^3 x=-\int g \nabla f \, d^3 x## provided that ##lim_{r \rightarrow \inf} [f(x)g(x)]=0## 3) Calculate the integral ##\int...- astrocytosis
- Thread
- Density of states Gradient Integral Integration Mechanics Quantum mechanics Vector calculus Volume Volume integral
- Replies: 2
- Forum: Advanced Physics Homework Help
-
M
I Why is this volume/surface integration unaffected by a singularity?
##\mathbf{M'}## is a vector field in volume ##V'## and ##P## be any point on the surface of ##V'## with position vector ##\mathbf {r}## Now by Gauss divergence theorem: \begin{align} \iiint_{V'} \left[ \nabla' . \left( \dfrac{\mathbf{M'}}{\left| \mathbf{r}-\mathbf{r'} \right|}... -

How to find the limits of a volume integral?
Homework Statement If ##\vec { F } = x \hat { i } + y \hat { j } + z \hat { k }## then find the value of ##\int \int _ { S } \vec { F } \cdot \hat { n } d s## where S is the sphere ##x ^ { 2 } + y ^ { 2 } + z ^ { 2 } = 4##. The Attempt at a Solution From gauss divergence theorem we know ##\int...- Hawkingo
- Thread
- Integral Limits Surface integral Triple integration Volume Volume integral
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-

Problem solving this volume using Jacobi's Determinant
Homework Statement Find the value of the solid's volume given by the ecuation 3x+4y+2z=10 as ceiling,and the cilindric surfaces 2x^2=y x^2=3*y 4y^2=x y^2=3x and the xy plane as floor.The Attempt at a Solution I know that we have to give the ecuation this form: ∫∫z(x,y)dxdy= Volume So, in fact...- JorgeM
- Thread
- Calculus 3 Determinant Jacobian Problem solving Volume Volume integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-

Calculate the volume integral of divergence over a sphere
Homework Statement For the vector field F(r) = Ar3e-ar2rˆ+Br-3θ^ calculate the volume integral of the divergence over a sphere of radius R, centered at the origin. Homework Equations Volume of sphere V= ∫∫∫dV = ∫∫∫r2sinθdrdθdφ Force F(r) = Ar3e-ar2rˆ+Br-3θ^ where ^ denote basis (unit vectors)...- Vitani11
- Thread
- Divergence Integral Sphere Volume Volume integral
- Replies: 13
- Forum: Advanced Physics Homework Help
-
A
How do integrals actually work?
Homework Statement Calculate the electrical energy required to assemble a spherical volume of radius R and charge Q, homogeneous density ρ the answer is (3/5)Q/R the textbook says you have to build the volume integral one layer of sphere at a time, I'll get back to that later. I like...- Aran Weizman
- Thread
- Calculus Electric energy Integrals Volume integral Work
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-

Volume integral of a function over tetrahedron
Homework Statement Calculate the volume integral of the function $$f(x,y,z)=xyz^2$$ over the tetrahedron with corners at $$(0,0,1) (1,0,0) (0,1,0) (0,0,1)$$ Homework Equations I was able to solve it mathematically, but still can't figure out why the answer is so small. I only understand...- physkim
- Thread
- Function Integral Tetrahedron Triple integral Volume Volume integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
R
How can a volume integral yield a vector field?
I'm using the textbook Electricity and Magnetism by Purcell. In the section about continuous charge distributions I found the following formula \mathbf{E}(x,y,z)= \frac{1}{4\pi\epsilon_0 } \int \frac{\rho(x',y',z')\boldsymbol{\hat r} dx'dy'dz'}{r^{2}} . It's stated that (x,y,z) is fixed...- rcmps772
- Thread
- Field Integral Vector Vector field Volume Volume integral Yield
- Replies: 8
- Forum: Other Physics Topics
-
D
How is the inverse of a volume integral denoted?
In 1-D the inverse of ∫ dx is dy/dx so how is the inverse of the volume integral ∫ d3x = ∫ dxdydz denoted ? Thanks -
F
How can divF=0, but the volume integral of divF=/=0
Homework Statement Basically, this is part C of a question where in part A we had to use the RHS of the divergence theorem below to calculate the LHS, and then in part B we had to calculate the divergene of F, which came to be 0. and part C asks us how can this be? Since in part A we used the...- FaraDazed
- Thread
- Integral Volume Volume integral
- Replies: 7
- Forum: Advanced Physics Homework Help
-
W
Volume integral in cylindrical coordinates
Homework Statement OK, I thought once I knew what the question was asking I'd be able to do it. I was wrong! Consider the volume V inside the cylinder x2 +y2 = 4R2 and between z = (x2 + 3y2)/R and the (x,y) plane, where x, y, z are Cartesian coordinates and R is a constant. Write down a triple...- whatisreality
- Thread
- Coordinates Cylindrical Cylindrical coordinates Integral Volume Volume integral
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
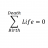
What is the closed volume integral symbol in Microsoft Word?
Hi everyone. I've been curious about a particular symbol, but I've never seen it used or mentioned in any context. I don't really have much information about its usage, so I thought I would ask around and see if anyone knew about its application. I saw this symbol in Microsoft word. How...- STEMucator
- Thread
- Integral Symbol Volume Volume integral
- Replies: 5
- Forum: Calculus
-

Volume of a quarter cylinder between 2 planes
Homework Statement Find the volume V of the region that lies inside the quarter cylinder 0 ≤ r ≤ 1, 0 ≤ θ ⇐ 1/2 π and between the planes x+y+z=4 and z=0, where (r, θ, z) are cylindrical polar coordinates. Homework Equations integral dV = integral r drdθdz The Attempt at a Solution I...- Matternot
- Thread
- Cylinder Planes Volume Volume integral
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
C
Integrating a delta function with a spherical volume integral
Homework Statement Integrate $$\int_V \delta^3(\vec r)~ d\tau$$ over all of space by using V as a sphere of radius r centered at the origin, by having r go to infinity. Homework EquationsThe Attempt at a Solution This integral actually came up in a homework problem for my E&M class and I'm...- counterpoint1
- Thread
- Delta Delta function Function Integral Spherical Spherical coordinates Volume Volume integral
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
J
Area and volume integral of vector field
In 2 dimensions given a scalar field f(x,y) is possible to compute the line integral ##\int f ds## and area integral ##\iint f d^2A##. In 3D, given a scalar field f(x,y,z) is possible to compute the surface integral ##\iint f d^2S## and the volume integral too ##\iiint f d^3V##...- Jhenrique
- Thread
- Area Field Integral Vector Vector field Volume Volume integral
- Replies: 4
- Forum: Differential Geometry
-
A
Volume integral turned in to surface + line integral?
Hi, I have a book that makes the equality. \vec{B}dV = (\vec{e_1}B_1 + \vec{e_2}B_2 + \vec{e_1}B_2)dx_1 dx_2 dx_3 \\[1ex] = dx_1 \vec{e}_1(B_1 dx_2 dx_3 ) + dx_2 \vec{e}_2(B_2 dx_1 dx_3 ) + dx_3 \vec{e}_3 (B_3 dx_1 dx_2) = (\vec{B}\cdot d\vec{S}) d\vec{l}. I'm a bit confused as to how it...- AntiElephant
- Thread
- Integral Line Line integral Surface Volume Volume integral
- Replies: 2
- Forum: Calculus
-
V
Volume Integral Orthogonal Polynomials
Hello. Homework Statement Basically I want to evaluate the integral as shown in this document: Homework Equations The Attempt at a Solution The integral with the complex exponentials yields a Kronecker Delta. My question is whether this Delta can be taken inside the integral...- VVS
- Thread
- Integral Orthogonal Polynomials Volume Volume integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
P
How can I solve a volume integral question with a trig substitution?
Hi, I was attempting a volume integral question out of a book. I know what the final answer is and what integral i am supposed to work out but I do not know how I am supposed to solve it. I have tried different ways such as integration by substitution and integration by parts but I do not seem... -
Y
Question regarding surface and volume integral
In page 3 of this articlehttp://faculty.uml.edu/cbaird/95.657%282012%29/Helmholtz_Decomposition.pdf I have two question: I use ##\vec r## for ##\vec x## and ##\vec r'## for ##\vec x'## in the article. \vec F(\vec r)=\frac {1}{4\pi}\nabla\left[\int_{v'}\nabla'\cdot\left(\frac{\vec F(\vec... -

Why is the volume integral of zero equal to zero?
If the integral of zero is a constant, then why is the volume integral of zero just zero?- tomwilliam2
- Thread
- Integral Volume Volume integral
- Replies: 3
- Forum: General Math
-
J
Volume Integral Set Up for Rotating Objects - Calculus Problem Explained
hi http://www.calcchat.com/book/Calculus-ETF-5e/ part b they want you to rotate it about the y-axis and in part c about the line x = 3. I don't understand this difference in writing for part b... 3^2 - (y^2)^2 And in part c they write (3-y)^2 I don't get it. It is chapter 7 section 2...- Jbreezy
- Thread
- Integral Set Volume Volume integral
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
U
Simple Volume Integral, limits of integration
Homework Statement Homework Equations The Attempt at a Solution Are my limits of integration right?- unscientific
- Thread
- Integral Integration Limits Limits of integration Volume Volume integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
A
A volume integral over a sphere
Homework Statement ∫∫∫∇.Fdv over x2+y2+z2≤25 F= (x2+y2+z2)(xi+yj+zk) Homework Equations ∫∫∫∇.Fdv = ∫∫ F.n dσ n=∇g/|∇g| The Attempt at a Solution g(x,y,z)=x2+y2+z2-25 taking the surface integral and replacing all (x2+y2+z2) with 25 i got 125 * ∫∫ dσ = 12500π But...- advphys
- Thread
- Integral Sphere Volume Volume integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
T
Some more volume integral questions
Formulas: Shell Method: dV = 2pi(radius) * (height) * (thickness) Disk method: dV = pi(radius)^2 * (thickness) Question 1 (26-3-15) Statement Using Shell method, find the volume generated by revolving the region bounded by the given curve about the x-axis. x = 4y - y^2 - 3, x = 0...- togo
- Thread
- Integral Volume Volume integral
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
V
Can volume of a rotated function be calculated using definite integrals?
Can I calculate the volume of any function rotated once about the y-axis by multiplying the definite integral of that function by 2*pi*r? For example if we want to generate a solid 3d shape from the function -x^2+1 we multiply the integral of it, (x - x^3 / 3), by 2*pi*1. The reason r is one in...- Vodkacannon
- Thread
- Integral Volume Volume integral
- Replies: 2
- Forum: Calculus
-
C
Field theory plane wave volume integral
Hi! I'm used to integrating over infinite spaces when working with QFT so far, but in an exercise I stumbled across a statement that \int_V d^3x e^{-i \vec x \cdot (\vec p - \vec p')} = V \delta_{\vec p \vec p'} It is clear that this is okay when p = p', but it does not seem to make sense...- center o bass
- Thread
- Field Field theory Integral Plane Theory Volume Volume integral Wave
- Replies: 5
- Forum: Quantum Physics
-
E
Volume integral of an ellipsoid with spherical coordinates.
Homework Statement By making two successive simple changes of variables, evaluate: I =\int\int\int x^{2} dxdydz inside the volume of the ellipsoid: \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=R^{2} Homework Equations dxdydz=r^2 Sin(phi) dphi dtheta dr The...- epiclier
- Thread
- Coordinates Ellipsoid Integral Spherical Spherical coordinates Volume Volume integral
- Replies: 7
- Forum: Calculus and Beyond Homework Help
-
I
Area and Volume integral using polar coordinates
Hi I'm working on area and volume integrals. I was wondering, when you convert to do the integral in polar, cylindrical or spherical co-ordinates, is there a standard set of limits for the theta variable in each case? for example from 0 -pi for polar, 0-2pi for cylindrical? If not how... -
1
Calculating Soot Deposition in a Circular Pattern
Homework Statement The soot produced by a garbage incinerator spreads out in a circular pattern. The depth H(r) in millimeters, of the soot deposited each month at distance r kilometers from the incinerator is given by H(r) = 0.115e^(-2r) Write the definite integral for the amount of soot...- 1MileCrash
- Thread
- Homework Integral Volume Volume integral
- Replies: 9
- Forum: Calculus and Beyond Homework Help
-
G
How Do You Set the Integration Limits for x and y in a Cone's Volume Integral?
I have the cone x^2 + y^2 <= z^2 with |z| <= 2 The vector function F = (4x, 3z, 5y) With the divergence theorem I managed to reduce the equation to ∫∫∫ 4 dxdydz Now the problem is finding out the limits. I know z goes from 0 to 2, but what about x and y?- geft
- Thread
- Cone Integral Volume Volume integral
- Replies: 5
- Forum: Calculus and Beyond Homework Help
-
M
Representing a region as limits of a volume integral
Homework Statement i have the region given as being bounded by x2+y2=4 and z=0 and z=3. this problem asks to prove gauss divergence theorem for a given vector F Homework Equations The Attempt at a Solution As for the volume integral, i had no problem. But for the surface integral, how...- msslowlearner
- Thread
- Integral Limits Volume Volume integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
N
Volume integral with 3 formulas mmn 15 3a
find the volume inclosed by z=0 x=y and y^2+z^2=x ?? i am having trouble drawing it i know i should look on th shadow of it on the x-y plane and integrate by it i can project on every plane i want to and build the integral appropriatly i jast can't imagine this shape if i can find...- nhrock3
- Thread
- Formulas Integral Volume Volume integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
N
Volume integral with 3 formulas mmn 15 3a
find the volume inclosed by z=0 x=y and y^2+z^2=x i am having trouble drawing it i know i should look on th shadow of it on the x-y plane and integrate by it- nhrock3
- Thread
- Formulas Integral Volume Volume integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
L
Volume integral, how do I find the limits for my integral?
Homework Statement [PLAIN]http://img9.imageshack.us/img9/4537/unledow.png Homework Equations The Attempt at a Solution Hi, does anyone know how to find the integral that needs to be evaluated here? I can't understand how to find it from the region edit: Oh and this is from here, not a take...- LHS
- Thread
- Integral Limits Volume Volume integral
- Replies: 6
- Forum: Calculus and Beyond Homework Help
-
M
What is the meaning of the integral of volume?
I have been thinking about the meaning of integrals and derivatives. For instance, the area of a sphere is 4 pi r^2. I can get that. The derivative of the area is 8 pi r or 4 times the circumference of the sphere. The derivative of this is just 8 pi. I can kind of understand that too. Then you...- mljoslinak
- Thread
- Integral Volume Volume integral
- Replies: 2
- Forum: Calculus
-
C
Lower and upper limits for a volume integral
Homework Statement I read an e-book about the classical mechanics and didn't know how to find the lower and upper limits for a volume integral. Homework Equations Perhaps, it may be related to the use of similar triangle. The Attempt at a Solution I calculated the x value...- chrisyuen
- Thread
- Integral Limits Volume Volume integral
- Replies: 2
- Forum: Introductory Physics Homework Help
-
J
Volume Integral for Vector Field in Spherical Coordinates
Homework Statement I'm stuck on the following vector integral Q(x)=INT[(p(y)/|x-y|)(dy)^3 For a sphere of uniform p (so it is not a function of y in this case). Where x is the position vector of a point lying outside the sphere and y is the position vector of a point lying inside the sphere...- jmz34
- Thread
- Integral Vectors Volume Volume integral
- Replies: 2
- Forum: Calculus and Beyond Homework Help
-
D
Volume integral of current density
Hi. Can anyone tell me what the volume integral of the current density is? I find it strange, but G.D. Mahan uses it in his book on page 30. He claims that this is in fact the current. I have attached the particular page.- daudaudaudau
- Thread
- Current Current density Density Integral Volume Volume integral
- Replies: 8
- Forum: Quantum Physics
-
S
Volume integral to spherical coords to contour integral
Homework Statement V(x) = \int \frac{d^3q}{(2\pi)^3} \frac{-g^2}{|\vec{q}|^2 + m^2} \exp^{i \vec{q} \cdot \vec{x}} = -\frac{g^2}{4\pi^2} \int_0^{\infty} dq q^2 \frac{exp^{iqr}-exp^{-iqr}}{iqr} \frac{1}{q^2+m^2} = \frac{-g^2}{4\pi^2 i r} \int_{-\infty}^{\infty} dq \frac{q...- sbh77
- Thread
- Contour integral Integral Spherical Volume Volume integral
- Replies: 4
- Forum: Calculus and Beyond Homework Help
-
I
How Do You Calculate the Mass of a Cone Using Volume Integrals?
Homework Statement "A solid cone is bounded by the surface \theta=\alpha in spherical polar coordinates and the surface z=a. Its mass density is p_0\cos(\theta). By evaluating a volume integral find the mass of the cone. Homework Equations The Attempt at a Solution I can't figure...- implet
- Thread
- Cone Integral Volume Volume integral
- Replies: 1
- Forum: Calculus and Beyond Homework Help
-
D
Solving for Volume in a Complex Figure: Ostrogradsky and Spherical Coordinates
Volume Integral! Help! I need help with this: Find volume of figure bounded with surface (x^2+y^2+z^2+1)^2=8*(x^2+y^2) I tried Ostrogradsky, and spherical coordinate system with it, but I can't find boundaries... PLEASE! HELP ME!- DianaSagita
- Thread
- Integral Volume Volume integral
- Replies: 3
- Forum: Calculus and Beyond Homework Help
-
C
Calculate Volume of a Portion of Sphere with Given Constraints
Homework Statement Find the volume of the portion of the sphere x^2 + y^2 + z^2 = 4 for which y>1 (or equal to). Homework Equations I would like to do this using a triple integral. The Attempt at a Solution OK, so I tried integrating the element r^2sin(theta)drd(phi)d(theta)...- cpfoxhunt
- Thread
- Integral Volume Volume integral
- Replies: 8
- Forum: Calculus and Beyond Homework Help
-
B
Volume integral with two intersecting shapes
The question I am dealing with has to do with the volume contained by two intersecting shapes I have created this integral and can't find a reasonable way of solving it. What is the best approach to solve this: \int_{r=0}^{\pi/2}\int_{u=0}^{2\cos\theta} \sqrt{9-r^2} * r drdu=- bobsmiters
- Thread
- Integral Shapes Volume Volume integral
- Replies: 8
- Forum: Calculus
-

Compute Volume Integral of $\vec V = xe^{-r}\hat i$: What is 'r'?
I have this vector function: \vec V = xe^{-r}\hat i I have to obtain the volume integral: I = \int(\vec \nabla \cdot \vec V)d^3x What is that 'r' and how do I compute the volume integral?- Reshma
- Thread
- Integral Volume Volume integral
- Replies: 10
- Forum: Advanced Physics Homework Help
-
I
Calculate Volume of Enclosed Region with Cylindrical Coordinates
"Find the volume of the region enclosed between the survaces z=x^2 + y^2 and z=2x" I figured that the simplest way of doing this was to switch to a cylindrical co-ordinate system. Can someone check that the limits of integration are then -\frac{\pi}{2}\leq \theta \leq\frac{\pi}{2} 0\leq\ r...- Imo
- Thread
- Integral Volume Volume integral
- Replies: 3
- Forum: Introductory Physics Homework Help
-
J
What is the solution to this volume integral problem?
I'm have trouble trying to evaluate the volume integral (shown in question.gif). I've attempted integrating it a few different ways, either achieveing an answer of 3 or 5.75, and I'm not sure where I'm going wrong. (Some of what I've done is in attempted_solution.gif) Any comments...- johnwalton84
- Thread
- Integral Volume Volume integral
- Replies: 3
- Forum: Introductory Physics Homework Help