- #1
VantagePoint72
- 821
- 34
A quick Google search reveals that 1 Parsec = 3.08568025 × 10^16 meters.
I have read two different rephrasings of the definition of a parsec:
1) The distance one would have to be from two luminous objects separated by one Astronomical Unit in order for them to appear one second of arc apart
2) Being a contraction of PARallax SECond, it is the distance of a star that would appear to have a parallax of one second of arc as the Earth completes half a revolution around the Sun
My problem is that these two definitions seem to be incompatible. Please note that I am not trying to disprove one, simply find out where the error in my math is (or perhaps my understanding of these two definitions). My ultra high-tech MS Paint diagrams, attached, illustrate my problem.
Figure 1 shows the first definition:
Length L represents the length of a parsec, and can be easily calculated as it is the perpendicular bisector of the given isosceles triangle. The angle of the right triangle created would be half of an arc second, the adjacent side L and the opposite side 0.5 AU. A quick trig calculation show L to have a length of 206264.8 AU. As one AU=149 598 000 000 metres, one parsec equals 3.085680248 x 10^16 metres, matching the above stated value.
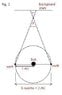
Figure 2 shows the second defintion:
Since the Earth's displacement over 6 months is 2 earth-sun distances, the base of this triangle is 2 Astronomical Units. 1" is the apparent parallax of the plotted star and by the Opposite Angle Theorem we see that theta must also equal 1". Now we have an isosceles triangle like above only while the angle remains the same, the base is twice the length. One need not go through to the steps again (though you may of course do so if you wish) to see that this will give a length for the parsec twice the stated value.
What's going on here?
I have read two different rephrasings of the definition of a parsec:
1) The distance one would have to be from two luminous objects separated by one Astronomical Unit in order for them to appear one second of arc apart
2) Being a contraction of PARallax SECond, it is the distance of a star that would appear to have a parallax of one second of arc as the Earth completes half a revolution around the Sun
My problem is that these two definitions seem to be incompatible. Please note that I am not trying to disprove one, simply find out where the error in my math is (or perhaps my understanding of these two definitions). My ultra high-tech MS Paint diagrams, attached, illustrate my problem.
Figure 1 shows the first definition:
Length L represents the length of a parsec, and can be easily calculated as it is the perpendicular bisector of the given isosceles triangle. The angle of the right triangle created would be half of an arc second, the adjacent side L and the opposite side 0.5 AU. A quick trig calculation show L to have a length of 206264.8 AU. As one AU=149 598 000 000 metres, one parsec equals 3.085680248 x 10^16 metres, matching the above stated value.
Figure 2 shows the second defintion:
Since the Earth's displacement over 6 months is 2 earth-sun distances, the base of this triangle is 2 Astronomical Units. 1" is the apparent parallax of the plotted star and by the Opposite Angle Theorem we see that theta must also equal 1". Now we have an isosceles triangle like above only while the angle remains the same, the base is twice the length. One need not go through to the steps again (though you may of course do so if you wish) to see that this will give a length for the parsec twice the stated value.
What's going on here?
Attachments
Last edited: