- #1
karush
Gold Member
MHB
- 3,269
- 5
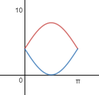
Use double integral to compute the area of the region
bounded by $y=4+4\sin{x}$ and $y=4-4\sin{x}$
on the interval $\left[0,\pi\right]$
View attachment 7253
ok it looks easier to do this in one $\int$ but it asks for a double $\int\int$ so ?
bounded by $y=4+4\sin{x}$ and $y=4-4\sin{x}$
on the interval $\left[0,\pi\right]$
View attachment 7253
ok it looks easier to do this in one $\int$ but it asks for a double $\int\int$ so ?