- #1
karush
Gold Member
MHB
- 3,269
- 5
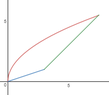
ok so there are 3 peices to this
Express and integral for finding the area of region bounded by:
\begin{align*}\displaystyle
y&=2\sqrt{x}\\
3y&=x\\
y&=x-2
\end{align*}
View attachment 7250
Express and integral for finding the area of region bounded by:
\begin{align*}\displaystyle
y&=2\sqrt{x}\\
3y&=x\\
y&=x-2
\end{align*}
View attachment 7250