1D Elastic Collision in CM frame

[stfz]

Hi all,
I've been self-studying a first year uni introductory mechanics course, and I'm confused with the derivations involved in calculating the final state of an elastic collision in one dimension, given the initial state.
So basically we have masses of m_1, m_2 with initial velocities v_1i, v_2i respectively that collide elastically.
The method I'm trying to understand is to use transformations to get into the CM frame.

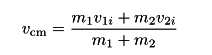
Transforming initial velocities into the CM frame:

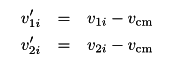
Given that momentum is conserved in the inertial coordinate frame (using the impulse approximation, we're assuming that CM frame is inertial... My first question - can someone explain why we can assume that CM frame is inertial? Is this because net force is reckoned equal to force of collision, which is an internal force?

Those assumptions then lead to:

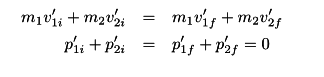
I.e. momentum conservation in the CM frame.
Now the next step I don't get:

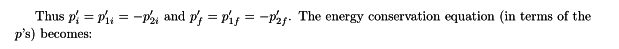
I'm assuming that $p'_i = p'_{1i}+p'_{2i}$ and similarly $p'_f=p'_{1f}+p'_{2f}$.
And $p'_i=p'_f=0$. But how can we state that $p'_i = p'_{1i}=-p'_{2i}$, etc. in the above. If my assumption was wrong, what are $p'_i, p'_f$ defined as?

Could someone please help me to understand how this works? I am using this course: https://www.phy.duke.edu/~rgb/Class/intro_physics_1/intro_physics_1.a4.pdf

Thanks in advance! :)

 

[Andrew Mason]

Hi all,]
Given that momentum is conserved in the inertial coordinate frame (using the impulse approximation, we're assuming that CM frame is inertial... My first question - can someone explain why we can assume that CM frame is inertial? Is this because net force is reckoned equal to force of collision, which is an internal force?

Yes. This is just an application of the first law: the assumption is that there are no external forces on the system.

Now the next step I don't get:
View attachment 94168
I'm assuming that $p'_i = p'_{1i}+p'_{2i}$ and similarly $p'_f=p'_{1f}+p'_{2f}$.
And $p'_i=p'_f=0$. But how can we state that $p'_i = p'_{1i}=-p'_{2i}$, etc. in the above. If my assumption was wrong, what are $p'_i, p'_f$ defined as?

Could someone please help me to understand how this works? I am using this course: https://www.phy.duke.edu/~rgb/Class/intro_physics_1/intro_physics_1.a4.pdf

$p'_i= p'_f=0$ applies in the CM frame. $p_f = p_{1f} + p_{2f} \ne 0$ and $p_i= p_{1i} + p_{2i} \ne 0$ applies in the observer frame. The prime (') should be used to designate the CM frame.

AM

 

[PeroK]

Now the next step I don't get:
View attachment 94168
I'm assuming that $p'_i = p'_{1i}+p'_{2i}$ and similarly $p'_f=p'_{1f}+p'_{2f}$.
And $p'_i=p'_f=0$. But how can we state that $p'_i = p'_{1i}=-p'_{2i}$, etc. in the above. If my assumption was wrong, what are $p'_i, p'_f$ defined as?

Could someone please help me to understand how this works? I am using this course: https://www.phy.duke.edu/~rgb/Class/intro_physics_1/intro_physics_1.a4.pdf

Thanks in advance! :)

What he's done is not what you assumed. He's defining $p'_i$ to be $p'_{1i}$. I can't really see a good reason to introduce another term for this momentum here, but that's what he's done. Just to emphasise that $p'_{1i} = - p'_{2i}$, perhaps. In any case, it's not the total momentum he's defined, as you assumed.