1st year high school geometry proof

[Iamconfused123]

Homework Statement

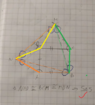
Above the sides AB and CD of paralelogram ABCD two equilateral triangle are formed ADN and DCM. Prove that triangle BMN is equilateral.

Relevant Equations

SAS - side, angle, side

I have proved that triangles around the equilateral triangle are congruent, but I don't know how to prove that they are arranged in such a way that they actually do form an equilateral triangle. Like, do I write that they do form an equilateral because it's given in the problem that triangles are drawn above the AD and CD sides and that because of that the vertices MNB are equally distanced from each other or? Or should I prove that triangle MNB has all angles of 60 degrees? But how do I do that, all I know for sure is that rectangle has 90 degree angles and that triangles ADN and DCM have 60 degree interior angles.

photo is in the attatchments

Thank you

 

[jedishrfu]

What's the definition of an equilateral triangle?

You have three triangles ABN, BCM, DMN. What can you say about them?

The angle NDM can be computed by 360-60-60-90

 

[Iamconfused123]

What's the definition of an equilateral triangle?

You have three triangles ABN, BCM, DMN. What can you say about them?

They have all same sides and all same angles

EDIT: Equilateral has all same sides and all same angles. And these 3 are congruent, they are the same.

 

[jedishrfu]

You can now say you have three equal sides and three equal angles hence you have an ______ triangle.

 

[Iamconfused123]

The angle NDM can be computed by 360-60-60-90

I mean, yes, I know. But, like, I still don't know these angles(circled ones)

 

[jedishrfu]

I don't think you need them.

The three dashed lines are all equal and share the three points B, M, and N. Hence you have an equilateral triangle

Equilateral triangles have three properties:
1) three sides are equal
2) three interior angles are equal and hence are 60 degrees
3) there are three lines of symmetry

Just by knowing it's an equilateral triangle from the sides and you know it has three 60-degree angles.

 

[neilparker62]

So NB=BM=MN qed.

 

[Iamconfused123]

Yes, but for example, what if we had 3 congruent triangles not connected by parallelogram and triangles on the sides of paralelogram, we'd still have three congruent triangles, but they wouldn't form equilateral triangle.

I know that there is equilateral triangle, the scheme is there, all sides equal, all angles equal. But how do I prove that other three triangles are position in such a way that they actually do form an equilateral triangle, since that is the base of our proof(proof is based on the fact that other three triangles are congruent and positioned in a proper way, we have proved that they are congruent , but how do we prove that they are positioned in such a way that they actually form eqlat triangle, we don't know other two angles and they seem to be pretty similar, we can't know for sure).

I feel like I am supposed to explain that the triangle is eqlat with information given in the problem. Like, it's eqlat because eqlat triangles on the sides of the parallelogram form a shape that makes eqlat triangle when NBM points are connected.

It's not so much how can I prove that NBM is qlat triangle, more of a what should I give as a reason for concluding so. If I say because these three are congruent then I need to know how are they positioned and I don't know the angles. The other explnanation would be; because that is the property of the shape we have gotten by drawing eqlat triangles on the side of parallelogram.

 

[neilparker62]

If you prove 3 sides of a triangle are all equal , then it's an equilateral triangle. And you have proven - you are done!

 

[FactChecker]

I mean, yes, I know. But, like, I still don't know these angles(circled ones)

You should be more careful. The bottom line of your diagram starts with triangle NAD. Shouldn't that be NAB? One thing you learn in math is to be very careful. It's a learned skill.

 

[Iamconfused123]

If you prove 3 sides of a triangle are all equal , then it's an equilateral triangle. And you have proven - you are done!

Thanks :)

 

[Iamconfused123]

You should be more careful. The bottom line of your diagram starts with triangle NAD. Shouldn't that be NAB? One thing you learn in math is to be very careful. It's a learned skill.

It is NAB, not sure what you refer to

 

[FactChecker]

It is NAB, not sure what you refer to

Did you take a close look at the hand-written work you posted? That sure looks like NAD to me.

 

[Iamconfused123]

Did you take a close look at the hand-written work you posted? That sure looks like NAD to me.

Oh, I see now. I was looking at the sketch, there is all fine, didn't even check the writing. I should be more careful. Thanks

 

[neilparker62]

Strictly speaking we should write: $$\Delta NAB \cong \Delta BCM \cong \Delta NDM\;SAS$$ Letter order is important when you are indicating either congruency or similarity of two or more triangles.