Sam Jelly
- 15
- 1
- Homework Statement
- Two identical masses m are attached by a spring of constant k in the vertical axis.
Determine the minimum compression of the spring so that when it is released the bottom mass is slightly off the ground.
- Relevant Equations
- MAcm = Fexternal
I am trying to solve this problem without using energy conservation. How can I solve this using the 2 body system and center of mass.
I know that in order for mass m at the bottom to be slightly off the ground the reaction force must be equal to zero. I don’t know if the reaction force before releasing the spring is equal to after it is released.
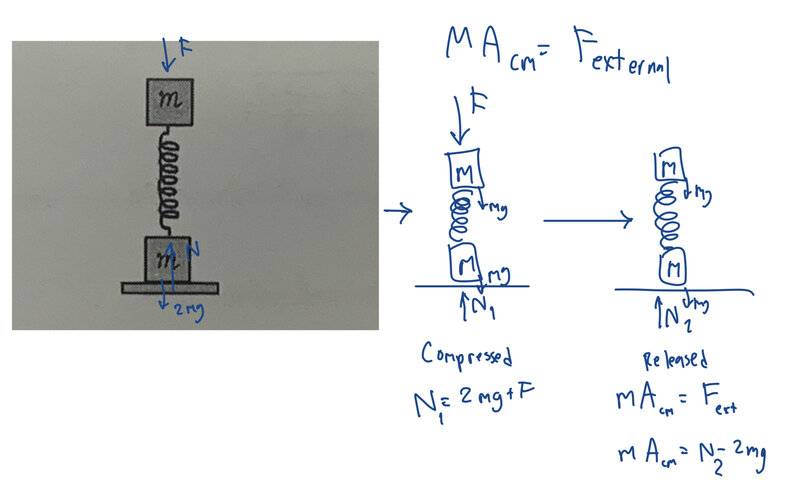
I know that in order for mass m at the bottom to be slightly off the ground the reaction force must be equal to zero. I don’t know if the reaction force before releasing the spring is equal to after it is released.