2 pullies and 3 masses -Tension

Click For Summary

Homework Help Overview

The discussion revolves around a system involving two pulleys and three masses, focusing on the tension in the strings connecting the masses. The original poster questions whether the tension remains constant throughout the string in this configuration, given the presence of multiple masses and pulleys.

Discussion Character

  • Exploratory, Assumption checking, Conceptual clarification

Approaches and Questions Raised

  • Participants explore the concept of tension in a multi-mass pulley system, questioning whether the tension is the same at all points in the string. Some suggest that the presence of a middle mass may lead to different tension values.

Discussion Status

The discussion is active, with participants providing insights into the conditions of the system, such as equilibrium and the forces acting on the masses. There is acknowledgment that the tensions may not be equal, and some participants have offered guidance on analyzing the forces involved.

Contextual Notes

Participants are considering the implications of different mass values and the setup of the system, including the need for free body diagrams and the effects of adding additional strings to the configuration. The discussion is framed within the context of homework help, emphasizing the need for clarity on given conditions and required outcomes.

Tesla In Person
Messages
34
Reaction score
13
Homework Statement
not a homework
Relevant Equations
t=mg
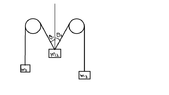
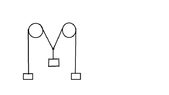
Hi, If i have a system that consists of 2 pullies and 3 masses, what is the tension on each part of the string? I know that for 2 masses hanging on either side of a pulley, the tension is the same. But for 3 masses, and 2 ideal pullies(no friction) and inextensible string, is tension the same too at every point on the string? I have attached a diagram to explain the problem.
 

Attachments

  • Untitled.png
    Untitled.png
    5.2 KB · Views: 205
Physics news on Phys.org
The tensions need not be the same because the string seems not to be continuous at the middle mass. It looks like you have two separate strings attached to the same point on ##m_2.##

If this is not homework, please do not post on the Homework forum.
 
kuruman said:
The tensions need not be the same because the string seems not to be continuous at the middle mass. It looks like you have two separate strings attached to the same point on ##m_2.##

If this is not homework, please do not post on the Homework forum.
ok so we have 2 different values for T in this case? Sorry I'm new to this website.
 
Tesla In Person said:
ok so we have 2 different values for T in this case? Sorry I'm new to this website.
If it's related to your schoolwork or studies, it's probably okay here in the schoolwork forums. If it is a practical problem where you are trying to lift something in your shop or at work, let me know and I can move it to the technical forums.

You need to start by drawing a Free Body Diagram of ##m_2##. Can you show us that FBD? Is the system stable or in motion?
 
berkeman said:
If it's related to your schoolwork or studies, it's probably okay here in the schoolwork forums. If it is a practical problem where you are trying to lift something in your shop or at work, let me know and I can move it to the technical forums.

You need to start by drawing a Free Body Diagram of ##m_2##. Can you show us that FBD? Is the system stable or in motion?
there are 3 forces acting on m2 , t1 t2 and it's weight. I'm not sure if t1 and t2 are equal or not. That's why i posted this question. I know for a single pulley system, the tension is the same on both sides but here we have 2 pullies and 3 masses.
fbd.png
 
Does ##m_2## accelerate? If not, what must be true about the forces acting on it?
 
Tesla In Person said:
there are 3 forces acting on m2 , t1 t2 and it's weight. I'm not sure if t1 and t2 are equal or not. That's why i posted this question. I know for a single pulley system, the tension is the same on both sides but here we have 2 pullies and 3 masses.
View attachment 333466
forces.png

Here's the figure with all the forces, t1 is same on either side of pulley(I'm treating it as if it was a 2 mass system so tension is the same on both sides) and t2 same on either side for the second pulley. That's what I did initially. I'm not sure if it's correct.
 
Reply
  • Like
Likes   Reactions: berkeman
kuruman said:
Does ##m_2## accelerate? If not, what must be true about the forces acting on it?
forces in y direction must be balanced i.e m2g= t1 cos a1 + t2 cos a2.
the tensions are reversed in my FBD, t1 is on the left and t2 on the right.
 
Can you figure out the values for ##T_1## and ##T_2##?
 
  • #10
Do you have a system in equilibrium (static problem) or the bodies are moving?
 
  • #11
nasu said:
Do you have a system in equilibrium (static problem) or the bodies are moving?
The system is in equilibrium.
 
  • #12
Thank for clarifying the conditions. This is important. Now you need to specify what is given and what is required for this problem. The original question was answered, the two tensions don't have to be equal.
 
  • #13
Tesla In Person said:
View attachment 333468
Here's the figure with all the forces, t1 is same on either side of pulley(I'm treating it as if it was a 2 mass system so tension is the same on both sides) and t2 same on either side for the second pulley. That's what I did initially. I'm not sure if it's correct.

You diagram is correct.
Now, imagine what would happen if ##m_1=0##.
Alternatively, imagine ##m_3=0##.

Can you see that the tensions do not need to be equal in order to achieve balance?
They would only happen in a symmetric case, where ##m_1=m_3##.

Going back to your diagram, decompose each tension in horizontal and vertical components.
Then, do a summation of horizontal and vertical forces.

Please, see:
https://courses.lumenlearning.com/s...apter/6-1-solving-problems-with-newtons-laws/

:cool:

CNX_UPhysics_06_01_StopLight.jpg
 
Reply
  • Informative
Likes   Reactions: Tesla In Person
  • #14
kuruman said:
Can you figure out the values for ##T_1## and ##T_2##?
sum of forces on m1 = ma so T1 - m1g = 0
T1 = m1g and T2=m2g.
 
  • #15
Yes. That says that the tensions are not equal unless the hanging masses are equal. The pulleys are assumed to be ideal which means that they change the direction of the tension but not its magnitude.
 
Reply
  • Like
Likes   Reactions: Tesla In Person
  • #16
kuruman said:
Yes. That says that the tensions are not equal unless the hanging masses are equal. The pulleys are assumed to be ideal which means that they change the direction of the tension but not its magnitude.

That says that the tensions are not equal unless the hanging masses are equal.

But for a one pulley and 2 masses system in equilibrium, if the 2 masses are different, we still have the same tension? So that only applies to this example where the tensions are equal in magnitude if the masses 1 and 3 are equal.
 
  • #17
I'm wondering if we had another string connected to m2 like I've shown in the diagram we would have to introduce another tension T3? And that tension would depend on the mass m2 only or It would be affected by the tensions T1 and T2 and we would get some other value? Because if I work out the tension T3 for the system in equilibrium I get: T3=m2g. So even though that middle string is connected to strings of tensions T1 and T2 these 2 won't affect the tension in the middle string?
 

Attachments

  • Untitled.png
    Untitled.png
    3.3 KB · Views: 131
  • #18
Tesla In Person said:
But for a one pulley and 2 masses system in equilibrium, if the 2 masses are different, we still have the same tension?
Yes, but in the case of different masses if the masses are accelerating, the tension is something in between the weights. If the masses are equal the tension is equal to the weight of either mass.

You have described the Atwood machine.
Tesla In Person said:
So that only applies to this example where the tensions are equal in magnitude if the masses 1 and 3 are equal.
For the 3-mass 2-pulley system shown in post #1, as long as the system is in equilibrium, the tension in each string will be equal to the weight hanging from it regardless of whether the masses are equal or not. However, when the masses are equal, the angles are equal ##\theta_1=\theta_2## which will not be the case when the masses are different.
 
Reply
  • Informative
Likes   Reactions: Tesla In Person
  • #19
Tesla In Person said:
I'm wondering if we had another string connected to m2 like I've shown in the diagram we would have to introduce another tension T3? And that tension would depend on the mass m2 only or It would be affected by the tensions T1 and T2 and we would get some other value? Because if I work out the tension T3 for the system in equilibrium I get: T3=m2g. So even though that middle string is connected to strings of tensions T1 and T2 these 2 won't affect the tension in the middle string?
Yes. Adding a string to ##m_2## will not affect the fact that T1 and T2 add as vectors to give a resultant that is equal to the weight.
 
Reply
  • Like
Likes   Reactions: Tesla In Person

Similar threads

Tension Question with One Mass and Two Pulleys
  • · Replies 7 ·
Replies
7
Views
2K
Ideal Vs Real Mass Pulley system
  • · Replies 10 ·
Replies
10
Views
5K
Pulley, two masses and an incline
  • · Replies 10 ·
Replies
10
Views
2K
Tension in a complex-pulley-system
  • · Replies 27 ·
Replies
27
Views
3K
Tension in a string which connects 3 pulleys
  • · Replies 12 ·
Replies
12
Views
1K
Problem with pulleys - two fixed and one movable
  • · Replies 22 ·
Replies
22
Views
2K
3 pulley problem with attached masses
  • · Replies 15 ·
Replies
15
Views
6K
Angular Velocity: Pulley and belt system
  • · Replies 11 ·
Replies
11
Views
4K
Finding acceleration of the pulley block system
  • · Replies 23 ·
Replies
23
Views
3K
Newton's Second Law (Pulley Sustem)
  • · Replies 3 ·
Replies
3
Views
2K