205.2.6.1-2 another implicit problem with tangent line.

In summary, the numbers 205.2.6.1-2 are most likely referring to a specific point or equation on a graph that is being analyzed in relation to tangent lines. Implicit problems with tangent lines refer to situations where the equation of a curve or function is not explicitly given, and finding the tangent line can help solve these problems by approximating the slope and determining the equation at a specific point. Other implicit problems can arise with tangent lines, and they can be solved using techniques such as implicit differentiation or the chain rule, as well as visually analyzing the graph.
  • #1
karush
Gold Member
MHB
3,269
5
Find the slope of the curve at the given point}
$2y^8 + 7x^5 = 3y +6x \quad (1,1)$
Separate the variables
$2y^8-3y=-7x^5+6x$
d/dx
$16y^7y'-3y'=-35x^4+6$
isolate y'
$\displaystyle y'=\frac{-35x^4+6}{16y^7-3}$
plug in (1,1)
$\displaystyle y'=\frac{-35(1)^4+6}{16(1)^7-3}=-\frac{29}{13}=m$
so equation of tangent line is
$\displaystyle y=-\frac{29}{13}(x-1)+1$

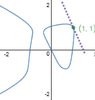
well at least the graph seemed ok
 

Attachments

  • 205_2_6_1-2.PNG
    205_2_6_1-2.PNG
    4.8 KB · Views: 105
Physics news on Phys.org
  • #2
Looks good to me. :)
 

FAQ: 205.2.6.1-2 another implicit problem with tangent line.

What is the meaning of "205.2.6.1-2" in the problem?

The numbers "205.2.6.1-2" represent a specific point on a graph or function. It is likely referring to the x-coordinate of the point.

What does "implicit problem" mean in this context?

In mathematics, an implicit problem refers to a problem where the relationship between variables is not explicitly stated. In other words, the equation or function is not given in a straightforward form, and the relationship between variables must be determined through other means.

How does the concept of tangent lines relate to the implicit problem in this case?

Tangent lines are used to approximate the slope of a curve at a specific point. In an implicit problem, the equation or function is not given in a straightforward form, making it difficult to find the slope at a specific point. Tangent lines can be used to estimate the slope in these cases.

Can you provide an example of an implicit problem with tangent line?

Sure, consider the equation x^2 + y^2 = 25. This equation is not explicitly solved for y, making it an implicit problem. To find the slope of the curve at a specific point, we can use the concept of tangent lines.

What are some common strategies for solving implicit problems with tangent lines?

One common strategy is to use the implicit differentiation method, where the derivative of the implicit equation is taken with respect to the variable of interest. Another strategy is to use the point-slope form of a line to find the slope at a specific point on the curve.

Similar threads

MHB Implicit Differentiation to find equation of a tangent line
Replies
4
Views
2K
MHB 210 AP Calculus Exam problem tangent line to curve
Replies
2
Views
1K
MHB 3.2.15 mvt - Mean value theorem: graphing the secant and tangent lines
Replies
3
Views
2K
MHB -apc.4.1.2 Find the slope at x=4
Replies
7
Views
2K
MHB 8.2.2 Int area of a region and graph
Replies
1
Views
966
MHB What is the equation of the tangent line at (π/2,1) for sin(xy)=y?
Replies
2
Views
2K
MHB Finding Intersection Points Between Circle & Line
Replies
4
Views
2K
MHB Calculating the Derivative of a Function Using the Chain Rule
Replies
2
Views
1K
MHB Differentiation and Tangent Lines.
Replies
13
Views
4K
MHB Implicit function theorem for f(x,y) = x^2+y^2-1
Replies
1
Views
1K

Hot Threads

Recent Insights

Back
Top