243 parametric equations and motion direction

[karush]

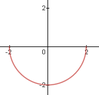
11.1 Parametric equations and a parameter interval for the motion of a particle in the xy-plane given. Identify the paritcals path by finding a Cartestian equation for it $x=2\cos t, \quad 2 \sin t, \quad \pi\le t \le 2\pi$
(a) Identify the particles path by finding a Cartesian Equation the Cartesian equation is
$$x^2+y^2=4$$
(b) Indicate the portion of the graph traced by the particle and the direction of motion
so if $x=2cos{(\pi)}=-2$ and $x=2cos{(2\pi)}=2$ then
$$-2\le t \le 2$$
and the particle moves in a clockwise directionView attachment 9217

ok, I think this is correct but I got the carresian equation just by ploting the parametric into desmos and saw that it was a circle with a radius of 2. the examples didn't the normal steps

also obviously I just pluged into see the direction of motion so...

I was going to try to use tikx on this but didn't how to use an interval be cute to put an arrow also

 

[HallsofIvy]

Did you really need to use "desmos"? If x= 2 cos(t) and y= 2 sin(t) then x^2= 4 cos^2(t) and y^2= 4 sin^2(t) so x^2+ y^2= 4cos^2(t)+ 4sin^2(t)= 4(cos^2(t)+ sin^2(t))= 4, the equation of a circle of radius 2. When t= \pi, x= 2 cos(\pi)= -2, y= 2 sin(\pi)= 0 and when t= 2\pi, x= 2 cos(2\pi)= 2, y= 2 sin(2\pi)= 0 so the particle moves counter-clock wise from (-2, 0) to (2, 0). You say "-2\le t\le 2". I am sure you mean "-2\le x\le 2".

 

[karush]

Ok I didn't understand how the square got there

View attachment 9218

Why is the text encroaching

 

[HallsofIvy]

Do you mean x^2 and y^2? They "got there" because I put them there!

And I put them there because I wanted an equation in x and y only. I wanted to eliminate "t" and I knew that, for any t, sin^2(t)+ cos^2(t)= 1.