244.14.4.8 Describe the given region in polar coordinates

[karush]

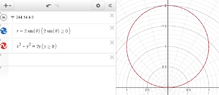
$\tiny{up(alt) 244.14.4.8}\\$
$\textsf{Describe the given region in polar coordinates}\\$
$\textit{a. Find the region enclosed by the semicircle}$
\begin{align*}\displaystyle
x^2+y^2&=2y\\
y &\ge 0\\
\color{red}{r^2}&=\color{red}{2 \, r\sin\theta}\\
\color{red}{r}&=\color{red}{2\sin\theta}
\end{align*}

View attachment 7692

ok
red is mine
but I thot this would be a semicircle when ploted
I think the polor equations is correct

 

[MarkFL]

We are given in rectangular coordinates:

$$x^2+y^2=2y$$

If we put this into standard circle form, we have:

$$x^2+y^2-2y=0$$

$$x^2+y^2-2y+1=1$$

$$x^2+(y-1)^2=1$$

 

[karush]

OK but isn't that still a circle and not a semicircle?

also,

standard circle form, isn't polar form?

 

[MarkFL]

OK but isn't that still a circle and not a semicircle?

Yes, now if you had been given another restriction, such as (but not necessarily limited to):

• $$x\ge0$$
• $$x\le0$$
• $$y\ge1$$
• $$y\le1$$

Then, you would have a semi-circle.

also,

standard circle form, isn't polar form?

I was referring to standard rectangular form:

$$(x-h)^2+(y-k)^2=r^2$$

 

[karush]

OK I think I am confused on this

The whole circle as given is $y \ge 0$

how do you get a semicircle from this?

if the center were $(0,0)$ then I could see that

 

[MarkFL]

OK I think I am confused on this

The whole circle as given is $y \ge 0$

how do you get a semicircle from this?

if the center were $(0,0)$ then I could see that

Well, we could write:

$$y=1\pm\sqrt{1-x^2}$$

Now, we must have:

$$-1\le\pm\sqrt{1-x^2}\le1$$

Hence:

$$0\le1\pm\sqrt{1-x^2}\le2$$

Or:

$$0\le y\le2$$

And so stating $0\le y$ would seem to be redundant.

 

[karush]

OK I see,

appreciate the help a lot...

started calc 4 but already worried!