3+1 split of the Electromagnetic Tensor and Maxwell's Equations

[jv07cs]

I'm currently studying the covariant formulation of electromagnetism for a research project I'm doing and I'm a bit a stuck on how to perform the 3+1 split of the Electromagnetic Field Tensor and Maxwell's Equations.

I understand that a 3+1 split of a four-vector consists of separating the temporal components from spatial components. For example, U⁰ = γc is the temporal component of 4-velocity and Uⁱ = γvⁱ are the spatial components of 4-velocity. But I don't know how I should perform this split for a rank 2 tensor, specifically the electromagnetic tensor, because I don't understand which would be it's temporal and spatial components and why.

I've read some places that F_0μ would be the temporal components and F_iμ the spatial componentes. But why? Is it because these are the components associated with the temporal and spatial componentes of the 4-force, respectively? And if that's correct, is the following the 3+1 split of the EM tensor?

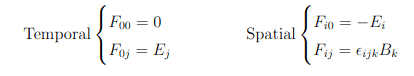
Also I'm stuck on how to perform the 3+1 split on Maxwell's Equations. What are the temporal and spatial components in the following equations?

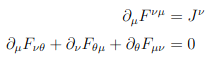
For the first equation, I would think I should just use the temporal components of F, which would give me Gauss's Law and Ampere's Law. But I have no idea on how to do it for the second equation.

I'm using the (-,+,+,+) signature and (ct, x, y, z) = (x⁰, x¹, x², x³) coordinates

 

[Dale]

I'm a bit a stuck on how to perform the 3+1 split of the Electromagnetic Field Tensor

Why would you do that? That doesn't make sense for anything other than rank 1 tensors (vectors). And even there it doesn't always make sense.

A 3+1 split sometimes works for a tensor with 4 components (vector), but it will never work for a tensor with 1 component (scalar) or tensors with 16 or more components (rank 2 and higher)

 

[Sagittarius A-Star]

But I don't know how I should perform this split for a rank 2 tensor, specifically the electromagnetic tensor, because I don't understand which would be it's temporal and spatial components and why.

Leonard Susskind writes in chapter 6.4 "Interlude on the Field Tensor", page 252 of the book "Special Relativity and Classical Field Theory", that the elements in the topmost row and the leftmost column (the electric field components) can be thought of as "mixed" space and time components. One of their indices is a time index, while the other is a space index.

 

[jv07cs]

Why would you do that? That doesn't make sense for anything other than rank 1 tensors (vectors). And even there it doesn't always make sense.

A 3+1 split sometimes works for a tensor with 4 components (vector), but it will never work for a tensor with 1 component (scalar) or tensors with 16 or more components (rank 2 and higher)

Yeah, I'm quite confused on how that would work and what would the "3+1 split of a rank 2 tensor" mean. But one of the assignments I received from my advisor was to "study the electromagnetic tensor in special relativity's spacetime and perform its 3+1 split".

I believe the idea is to show that electric and magnetic fields are a part of the same field, the electromagnetic field tensor, and only exist separately when a 3+1 split is performed.

 

[jv07cs]

Leonard Susskind writes in chapter 6.4 "Interlude on the Field Tensor", page 252 of the book "Special Relativity and Classical Field Theory", that the elements in the topmost row and the leftmost column (the electric field components) can be thought of as "mixed" space and time components. One of their indices is a time index, while the other is a space index.

Thanks for the reference. So if I have these "mixed" components, a 3+1 split of the tensor would be only F₀₀ for the temporal part and F_ij for the spatial part? I'm still very confused.

 

[Sagittarius A-Star]

Thanks for the reference. So if I have these "mixed" components, a 3+1 split of the tensor would be only F₀₀ for the temporal part and F_ij for the spatial part? I'm still very confused.

I think, according to the logic of Susskind, pure spatial components would be the elements in the 3 x 3 matrix, that excludes the topmost row and the leftmost column. That would be the magnetic field components.

 

[jv07cs]

Regarding the 3+1 split of Maxwell's Equations, I think the question might be better formulated in this exercise of Kip Thorne's "Modern Classical Physics":

And equation (2.48) it refers to is:

If anyone could give me little help on how to do this.

 

[Dale]

one of the assignments I received from my advisor was to "study the electromagnetic tensor in special relativity's spacetime and perform its 3+1 split"

I think you need to talk to your advisor. This assignment doesn't make any sense. One issue is that not all coordinate systems have one time and three space components. So this split cannot be done in all coordinate system even for a four-vector. The other issue is that even in coordinate systems with one time and three space components, for a rank 2 tensor there are 6 components that have indices that mix both time and space components. This assignment is not a good assignment in my opinion, as presented. The advisor should clarify the assignment and the purpose of the assignment.

Thanks for the reference. So if I have these "mixed" components, a 3+1 split of the tensor would be only F₀₀ for the temporal part and F_ij for the spatial part? I'm still very confused.

You need to talk to your advisor.

 

[jv07cs]

I think you need to talk to your advisor. This assignment doesn't make any sense. One issue is that not all coordinate systems have one time and three space components. So this split cannot be done in all coordinate system even for a four-vector. The other issue is that even in coordinate systems with one time and three space components, for a rank 2 tensor there are 6 components that have indices that mix both time and space components. This assignment is not a good assignment in my opinion, as presented. The advisor should clarify the assignment and the purpose of the assignment.

You need to talk to your advisor.

Right. I'll talk to him to clarify what he meant by that.About Maxwell's Equations 3+1 split as formulated in this exercise. Would you be able to help me with this part? Because they involve the electromagnetic tensor and I have no idea on how to perform the split if not performing it for each term.

Regarding the 3+1 split of Maxwell's Equations, I think the question might be better formulated in this exercise of Kip Thorne's "Modern Classical Physics":
View attachment 336577
And equation (2.48) it refers to is:
View attachment 336578

If anyone could give me little help on how to do this.

 

[Sagittarius A-Star]

About Maxwell's Equations 3+1 split as formulated in this exercise. Would you be able to help me with this part? Because they involve the electromagnetic tensor and I have no idea on how to perform the split if not performing it for each term.

You need tho write down equation (2.48) component-wise, see in the video at time 1h30m56s:

 

[Dale]

About Maxwell's Equations 3+1 split as formulated in this exercise. Would you be able to help me with this part?

I cannot help. To me, the whole concept of a 3+1 split on a rank 2 tensor doesn’t make any sense.

In all of my several years of experience using these tensors and working with electromagnetism I have never done this. It is completely baffling to me. I don’t understand either the “how” or the “why” for this assignment.

Sorry, I will bow out and hopefully someone else understands.

 

[jv07cs]

You need tho write down equation (2.48) component-wise, see in the video at time 1h30m56s:

Oh so this 3+1 split asked by the exercise would not be necessarily referring to separating temporal and time componentes of the equations, but just to write the equations in a specific inertial frame?

 

[jv07cs]

Oh so this 3+1 split asked by the exercise would not be necessarily referring to separating temporal and time componentes of the equations, but just to write the equations in a specific inertial frame?

If that's the case, I believe this same reasoning would be the idea behind the "
+1 split of the electromagnetic tensor". The tensor is the same object for every inertial frama and by "perform a 3+1 split" it would only mean to write the coordinates as measured by a specific reference frame and not to "separate the temporal and spatial components" of the tensor.

 

[Orodruin]

Splitting a rank 2 tensor in 1+3 generally makes little sense. A thing more analogous to what is going on when splitting a 4-vector 1+3 is to split a rank 2 tensor in its pure temporal (1x1), pure spatial (3x3), and mixed (1x3 or 3x1) parts. These are parts that transform as a scalar, a tensor, and vectors under the rotational subgroup of the Lorentz group (ie, excluding boosts).

Why is this of interest? Well, we are very used to this subgroup and hopefully we can gain some insight. For example, the 4-current density is a 4-vector that splits 1+3 into charge density and curremt density. Maxwell’s stress tensor is a rank 2 tensor that splits into EM energy density, the Maxwell stress tensor, and the Poynting vector, which are all familiar from electromagnetism. It is a good insight that these together form part of the same tensor in spacetime!

As for the field tensor, it is not just any rank 2 tensor. It is an antisymmetric rank 2 tensor! This means it has no purely temporal component and the purely spatial component is an antisymmetric rank 2 3-tensor, which means it transforms as a pseudo-vector under rotations! The vector from the mixed part is the electric field and the pseudo-vector from the purely spatial part is the magnetic field.

 

[Sagittarius A-Star]

Oh so this 3+1 split asked by the exercise would not be necessarily referring to separating temporal and time componentes of the equations, but just to write the equations in a specific inertial frame?

I guess, he means the following assignments to indices. But, as @Dale mentioned, you can ask him.

The equation (2.48) in posting #7 is:
$\partial_\gamma F_{\alpha \beta} + \partial_\alpha F_{\beta \gamma} + \partial_\beta F_{\gamma \alpha} = 0$

You can set $\alpha$, $\beta$ and $\gamma$ to any three of the four dimensions t, x, y, z (or 0, 1, 2, 3).
Take for example the spatial indices:
$\gamma = x$
$\alpha = y$
$\beta = z$
$\Rightarrow$
$\partial_x B_x + \partial_y B_y + \partial_z B_z = 0$, compare this divergence to left equation (2.50) in posting #7.

Take for example one temporal and two spatial indices:
$\gamma = y$
$\alpha = x$
$\beta = t$
$\Rightarrow$
$\partial_x E_y - \partial_y E_x + \partial_t B_z = 0$, this is the z-component of the right equation (2.50) in posting #7.

 

[phyzguy]

@Dale , I think you are misleading the OP by saying the assignment doesn't make any sense. To me it is an important piece of learning. As @Orodruin says, the fact that the rank-2 electromagnetic field tensor is anti-symmetric means the time components can be identified as a 3D vector - the electric field, and the space components can be identified as a 3D pseudovector - the magnetic field. It is important to understand this in order to understand how the 4D formulation of the electromagnetic field tensor is reduced to the classic Maxwell equations.
$$ \begin{bmatrix}
0 & Ex & Ey & Ez \\
-Ex & 0 & Bz & -By \\
-Ey & -Bz & 0 & Bx \\
-Ez & By & -Bx & 0
\end{bmatrix} $$

 

[PeterDonis]

the 3+1 split of Maxwell's Equations

Which, as the quote you give shows, does exist (once you've picked a frame), but which is not the same thing as a 3+1 split of the EM field tensor, which, as has already been noted, doesn't exist. If you make a 3+1 split of Maxwell's Equations, as the quote you give shows, you have to change your representation of the EM field from a 2nd rank antisymmetric tensor to two 3-vectors, the electric and magnetic field vectors. (More precisely, the electric field is a 3-vector and the magnetic field is a 3-pseudovector.)

If your advisor is asking you to do a 3+1 split of Maxwell's Equations, as is asked in what you quote from Thorne, then the question is fine and you just misstated it in the OP of this thread. But if your advisor is asking you to do a 3+1 split of the EM field tensor, not Maxwell's Equations, then, as has been said, that doesn't make sense and you should ask your advisor to clarify the question.

 

[PeterDonis]

I think you are misleading the OP by saying the assignment doesn't make any sense.

It depends on what the assignment actually was. At this point we don't know whether the actual assignment given to the OP by his advisor was to give a 3+1 split of the EM field tensor, as stated in the OP (which doesn't make sense), or whether it was actually to give a 3+1 split of Maxwell's Equations, as in the Thorne reference that was given (which does make sense, but means the OP misstated what the assignment was).

What we really need is for the OP to be more specific about exactly what his advisor asked him to do.

 

[phyzguy]

How does splitting the electromagnetic field tensor into the E and B vectors not make sense?

 

[Sagittarius A-Star]

About Maxwell's Equations 3+1 split as formulated in this exercise. Would you be able to help me with this part? Because they involve the electromagnetic tensor and I have no idea on how to perform the split if not performing it for each term.

Addition to posting #15:

You get the upper left equation (2.50) in posting #7 by calculating the time-component of the 4-current in the upper equation (2.48).
You get the upper right equation (2.50) in posting #7 by calculating the space-components of the 4-current in the upper equation (2.48).

 

[PeterDonis]

How does splitting the electromagnetic field tensor into the E and B vectors not make sense?

It does, but it doesn't make sense to describe doing this as a "3+1 split" of the tensor.

 

[jv07cs]

It depends on what the assignment actually was. At this point we don't know whether the actual assignment given to the OP by his advisor was to give a 3+1 split of the EM field tensor, as stated in the OP (which doesn't make sense), or whether it was actually to give a 3+1 split of Maxwell's Equations, as in the Thorne reference that was given (which does make sense, but means the OP misstated what the assignment was).

What we really need is for the OP to be more specific about exactly what his advisor asked him to do.

The assignment asks both. One of the exercises is to study the electromagnetic tensor in special relativity's spacetime and perform its 3+1 split, and the next exercise is to write maxwell's equations for the electromagnetic tensor and then obtain the form of these equations after the 3+1 split.

From the discussion in this thread, I believe that the idea behind this questions was to simply "chose" an inertial frame and write the tensor components as measured by such frame, then write the covariant form of Maxwell's Equations and then "chose" an inertial frame and write maxwell's equations with the quantities measured in this frame. In this sense, the "3+1" split in the question would mean "introduce a specific inertial frame into spacetime".

I don't know if that's correct, I might just have misunderstood this part of the assignment, but it kinda makes sense to me in this way looking at this paragraph in Kip Thorne's book:

 

[robphy]

Possibly useful
https://www.physicsforums.com/insig...rver-a-relativistic-calculation-with-tensors/
for some techniques of a decomposition with respect to a future-timelike 4-velocity.
Decomposing the field equations into the Maxwell Equations
is easier than the above (which effectively tries to write a transformation formula).

Sometimes, it's best to work in coordinates to see what is going on.
Then, work tensorially.

 

[PeterDonis]

The assignment asks both.

Hm. Then I think it's not a very well worded assignment, for reasons which have already been given.

One of the exercises is to study the electromagnetic tensor in special relativity's spacetime and perform its 3+1 split

Which, as has been said, makes no sense. When you do such a "split" for the EM field tensor, you don't get "3+1"--a scalar and a 3-vector. You get two 3-vectors (or more precisely a 3-vector and a 3-pseudovector).

the next exercise is to write maxwell's equations for the electromagnetic tensor and then obtain the form of these equations after the 3+1 split.

Which does make sense, but still, as noted, isn't well described as a "3+1 split".

it kinda makes sense to me in this way looking at this paragraph in Kip Thorne's book

That quote does describe what "3+1 split" implies, yes. But, as noted above, it then obviously doesn't make sense for the EM field tensor; what Thorne is describing in that quote is not what you get when you "split up" the EM field tensor in a particular inertial frame.

It might be worth nothing that there is an alternate way of formulating Maxwell's Equations, using a 4-vector potential instead of the EM field tensor. Since the 4-potential is a 4-vector, it does make sense to do a "3+1 split" on it: you get a scalar potential and a vector potential. The reason this is often not done is that the 4-potential (a) is not directly measurable, while the fields are; and (b) is not unique; there are many possible potential 4-vectors that give the same EM field tensor. (This is a consequence of gauge invariance, and picking one of the many possible 4-potentials is called "choosing a gauge".)

 

[robphy]

I think "3+1" is more about splitting "spacetime",
rather than splitting tensors into a vector-like object and a scalar-like object.
Upon splitting spacetime, one defines various parts of the tensor in terms of the split geometrical structures (e.g. projections onto hypersurfaces).
In some cases, it could result in a tensor decomposed into a vector-like object and a scalar-like object,..
but it need not be, as we see with the electromagnetic field tensor.

• https://doi.org/10.1093/acprof:eek:so/9780199205677.003.0002
  Ch 2 THE 3+1 FORMALISM
  Introduction to 3+1 Numerical Relativity
  Miguel Alcubierre
  

  (abstract)
  ... This chapter focuses on the 3+1 formalism, where spacetime is split into three-dimensional space on the one hand, and time on the other.

• https://arxiv.org/abs/gr-qc/0703035
  3+1 Formalism and Bases of Numerical Relativity
  Eric Gourgoulhon (LUTH, CNRS / Observatoire de Paris)
  

  (Ch 1 Introduction)
  The 3+1 formalism is an approach to general relativity and to Einstein equations that relies on the slicing of the four-dimensional spacetime by three-dimensional surfaces (hypersurfaces). These hypersurfaces have to be spacelike, so that the metric induced on them by the
  Lorentzian spacetime metric [signature (−, +, +, +)] is Riemannian [signature (+, +, +)].

• https://www34.homepage.villanova.edu/robert.jantzen/gem/
  Understanding Spacetime Splittings and Their Relationships or
  Gravitoelectromagnetism: the User Manual
  Robert T. Jantzen, Paolo Carini, and Donato Bini
  June 9, 2004
  
  
  
  Maxwell's Equations are discussed in Ch 4.
• Gravitation
  Misner, Thorne, Wheeler
  
  
  Maxwell's Equations are discussed in Ch 3.4.

---

UPDATE: There's also a 2+2 splitting

• https://arxiv.org/abs/gr-qc/9510040
  Covariant double-null dynamics: (2+2)-splitting of the Einstein equations
  P. R. Brady, S. Droz, W. Israel, S. M. Morsink
  
  

  The paper develops a (2+2)-imbedding formalism adapted to a double foliation of spacetime by a net of two intersecting families of lightlike hypersurfaces. The formalism is two-dimensionally covariant, and leads to simple, geometrically transparent and tractable expressions for the Einstein field equations and the Einstein-Hilbert action, and it should find a variety of applications. It is applied here to elucidate the structure of the characteristic initial-value problem of general relativity.

So,
3+1 is useful for the Cauchy Initial Value Problem (data given on a spacelike initial-data surface).
2+2 is useful for the Characteristic Initial Value Problem (data given on one or more null hypersurfaces).

 

[Sagittarius A-Star]

About Maxwell's Equations 3+1 split as formulated in this exercise. Would you be able to help me with this part?

Alternative to the calculation in my posting #15:

The bottom equation (2.48) of Kip Thorne in posting #7 is called "Bianchi Identity", according to Leonard Susskind. From my viewpoint, this is not the most intuitive starting point to derive the 3+1 notation of Maxwells equations.

If you look at equations (2.50) in posting #7, then you see, that the two bottom Maxwell's equation look almost equal as the two Maxwell's equation at the top, if you exchange E and B. The only difference is a sign and the fact, that the right sides of the equations are zero. That is, because no magnetic monopoles exist.

In the following video they derive first both top equations in (2.50) in posting #7 from the top equation (2.48), containing the EM field tensor:

$\partial_\beta F^{\alpha \beta} = \mu_0 J^\alpha$

Then they derive both bottom equations in (2.50) in posting #7. For this they use the dual tensor, wich is the EM field tensor, except an exchange of E and B, with additionally some sign changes:

$\partial_\beta G^{\alpha \beta} = 0$ (no magnetic monopoles)