3-link planar manipulator: a statics conceptual question

[Sunny Sun]

Not homework, but I hope this is the right forum to post in:

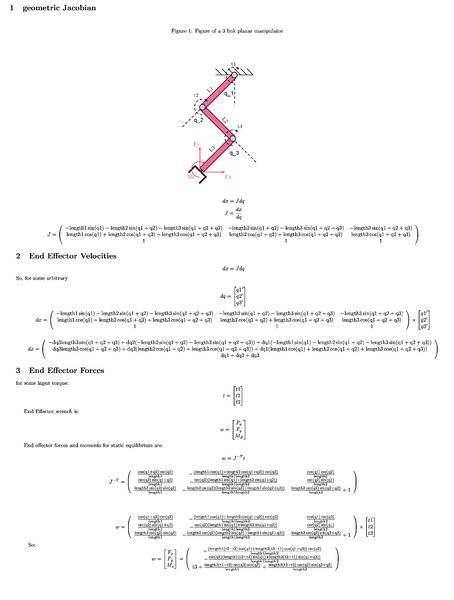
1. Homework Statement
So we have a 3-link planar manipulator, with lengths L1,L2,L3 and angles q1,q2,q3.
About each of the joints, we may apply a torque, t1,t2,t3.
At the end effector, there will be a force and moment that will fulfill static equilibrium with the input joint torques.

Homework Equations

So we can go through the rigmarole and compute the geometric jacobian, which is a map from your angular velocies to your linear endpoint velocities. dx = J dq.

From my image, you can see that the linear velocities care about the orientation of the 3rd limb.

Now, using the principles of virtual work, we can compute the end effector moment and forces that we need in order to balance the input torques.
W = J^-T t, where W is the end effector wrench and t is a joint torques vector and J^-T is the inverse transpose of J.
You can see from the analytical solution, that the Fx and Fy do not depend on the orientation q3 of the 3rd limb!

The Attempt at a Solution

if that image is too blurry:
https://i.redd.it/nmpd2ekfv3f11.jpg

A puzzling observation. Can someone explain why conceptually that the orientation of the 3rd link has no effect on the Fx and Fy, but does change the end effector moment Mz?

 

[Valkarie]

The answer lies in the fact that the end effector force Fx and Fy are only affected by the orientations of the first two links (q1,q2). This is because the Jacobian matrix describes how a change in joint angles affects the linear velocity of the end effector. Since the end effector force is related to the linear velocity, this means that the orientation of the third link has no influence on the linear velocity of the end effector and thus no influence on the corresponding forces. However, the orientation of the third link does affect the angular velocity of the end effector and thus the corresponding moment (Mz) as described in the Jacobian matrix.