patric44
- 308
- 40
- Homework Statement
- the arrangement in the figure
- Relevant Equations
- sum(F)=ma
in the opposite problem that has three pulleys and two masses, the book is asking for :
1- the tension on the string.
2- the acceleration of pulley p1.
3- the acceleration of mass m2.
4- what should the mass "m" be such that m1 does not accelerate?
note : pulley p1 has mass m, in the diagram of P1 there should be mg also along with T on pulley 1 , I assume!
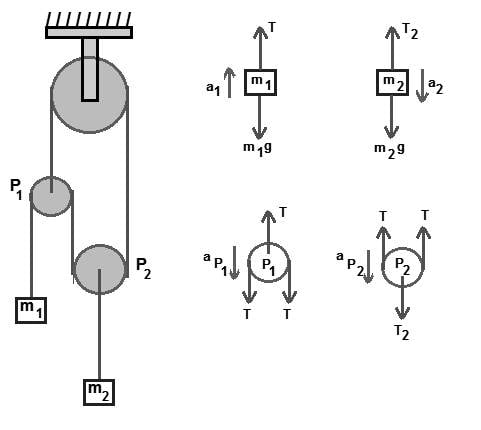
the solution
1-
$$
T-m_{1}g=m_{1}a_{1},\quad,\quad T=m_{1}(g+a_{1})
$$
2-
$$
m_{2}g-T_{2}=m_{2}a_{2},\quad,\quad a_{2}=(m_{2}g-T_{2})/m_{2}
$$
3-
$$
2T-T-mg=ma_{p1}\quad,\quad a_{p1}=T/m-g
$$
4- now for a_{1} to equal zero the system will be in equilibrium and
$$
T=m1g\quad, T/m=g\quad, m=m_{1}
$$
I just want to check my answer or if I am missing something, thanks in advance.
1- the tension on the string.
2- the acceleration of pulley p1.
3- the acceleration of mass m2.
4- what should the mass "m" be such that m1 does not accelerate?
note : pulley p1 has mass m, in the diagram of P1 there should be mg also along with T on pulley 1 , I assume!
the solution
1-
$$
T-m_{1}g=m_{1}a_{1},\quad,\quad T=m_{1}(g+a_{1})
$$
2-
$$
m_{2}g-T_{2}=m_{2}a_{2},\quad,\quad a_{2}=(m_{2}g-T_{2})/m_{2}
$$
3-
$$
2T-T-mg=ma_{p1}\quad,\quad a_{p1}=T/m-g
$$
4- now for a_{1} to equal zero the system will be in equilibrium and
$$
T=m1g\quad, T/m=g\quad, m=m_{1}
$$
I just want to check my answer or if I am missing something, thanks in advance.