- #1
mastrofoffi
- 51
- 12
Hello, I have been assigned to write a report on a topic of my choice for my Computational Physics class, and I chose to focus on the symplectic integration of Hamiltonian systems, in particular the Lotka-Volterra model.
A 3-species model([itex]\gamma[/itex] eats [itex]\beta[/itex], [itex]\beta[/itex] eats [itex]\alpha[/itex]) is not, unlike the classic Prey-Predator model, directly representable by an Hamiltonian since we have 3 coordinates, so I splitted my set of differential equations in a system of 2 coupled Hamiltonians, so from this
$$
\begin{cases}
\dfrac{dx}{dt} = x(A - By)\\
\dfrac{dy}{dt} = y(-C + Dx - Ez)\\
\dfrac{dz}{dt} = z(-F + Gy)\\
\end{cases}
$$
I obtained this:
\begin{cases}
H_1 = Be^y - Ay - Cx + De^x - Exe^z\\
H_2 = Ge^y - Fy + Cz + Ee^z - Dze^x\\
\end{cases}
where [itex]x=ln\alpha, y=ln\beta, z=ln\gamma[/itex]; in [itex]H_1[/itex] i consider [itex]z[/itex] to be instantaneously constant, and in [itex]H_2[/itex] I do the same for [itex]x[/itex]; all the interaction parameters are positive.
So in [itex]H_1[/itex] my hamiltonian variables are p=x q=y, while in the other they are p=y q=z.
I used a symplectic Euler method to integrate these equations(at every instant I first integrate H1 and then H2 with the newly obtained values for x and y; I also tried to invert the order of integration and there are no significative changes) and I manage to get some fairly nice orbits in 3d space
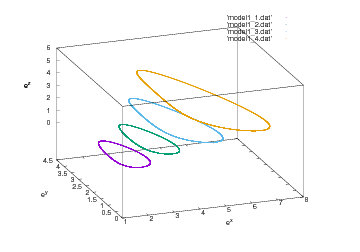
Here i used parameters A=B=C=D=E=F=G=1 and same starting conditions for every species (1, 2, 3, 4); the orbit gets larger as the starting number of individuals increases.
Now I tried to interpret these closed orbits as oscillations around a stable equilibrium point(as in the 2 species prey-predator case), and I made many different assumptions to try to find where this equilibrium points were located, but had no luck.
First of all I assumed that motions sharing the same "total Hamiltonian"(i know that the sum of these two hamiltonians is not the hamiltonian of the whole system, but I tried anyway) [itex]H = H1+H2[/itex] should be lying on the same surface, since H is a first integral of the motion, but to now I couldn't manage to verify nor to exclude this (I also tried to ask my Analysis professor, but she said she couldn't really help me with this, even though she said the assumption might be reasonable).
I also tried a more geometrical approach, seeing as the orbits seem to open up in some conical shape around a vertex, which should be a stable eq point, but had no luck with this either.
Again, solving the set of diff. equations, I found out that all the equilibrium points for this system should be on a straight line over plane y=1: [itex]z = x - 1[/itex] for my set of parameters
Even with this I could not associate any orbit with a specific point on the line.
I feel like I'm either lacking some fundamental mathematical knowledge to approach the problem of finding the barycenters of these orbits or I'm missing something very important.
I actually believe there may be some fallacies in my reasoning, especially in the Hamiltonian approach I used, which, even being correct(and I'm not even sure about this) from a purely computational standpoint, feels a bit weird from a physical point of view.
Any suggestion or help will be greatly appreciated
A 3-species model([itex]\gamma[/itex] eats [itex]\beta[/itex], [itex]\beta[/itex] eats [itex]\alpha[/itex]) is not, unlike the classic Prey-Predator model, directly representable by an Hamiltonian since we have 3 coordinates, so I splitted my set of differential equations in a system of 2 coupled Hamiltonians, so from this
$$
\begin{cases}
\dfrac{dx}{dt} = x(A - By)\\
\dfrac{dy}{dt} = y(-C + Dx - Ez)\\
\dfrac{dz}{dt} = z(-F + Gy)\\
\end{cases}
$$
I obtained this:
\begin{cases}
H_1 = Be^y - Ay - Cx + De^x - Exe^z\\
H_2 = Ge^y - Fy + Cz + Ee^z - Dze^x\\
\end{cases}
where [itex]x=ln\alpha, y=ln\beta, z=ln\gamma[/itex]; in [itex]H_1[/itex] i consider [itex]z[/itex] to be instantaneously constant, and in [itex]H_2[/itex] I do the same for [itex]x[/itex]; all the interaction parameters are positive.
So in [itex]H_1[/itex] my hamiltonian variables are p=x q=y, while in the other they are p=y q=z.
I used a symplectic Euler method to integrate these equations(at every instant I first integrate H1 and then H2 with the newly obtained values for x and y; I also tried to invert the order of integration and there are no significative changes) and I manage to get some fairly nice orbits in 3d space
Here i used parameters A=B=C=D=E=F=G=1 and same starting conditions for every species (1, 2, 3, 4); the orbit gets larger as the starting number of individuals increases.
Now I tried to interpret these closed orbits as oscillations around a stable equilibrium point(as in the 2 species prey-predator case), and I made many different assumptions to try to find where this equilibrium points were located, but had no luck.
First of all I assumed that motions sharing the same "total Hamiltonian"(i know that the sum of these two hamiltonians is not the hamiltonian of the whole system, but I tried anyway) [itex]H = H1+H2[/itex] should be lying on the same surface, since H is a first integral of the motion, but to now I couldn't manage to verify nor to exclude this (I also tried to ask my Analysis professor, but she said she couldn't really help me with this, even though she said the assumption might be reasonable).
I also tried a more geometrical approach, seeing as the orbits seem to open up in some conical shape around a vertex, which should be a stable eq point, but had no luck with this either.
Again, solving the set of diff. equations, I found out that all the equilibrium points for this system should be on a straight line over plane y=1: [itex]z = x - 1[/itex] for my set of parameters
Even with this I could not associate any orbit with a specific point on the line.
I feel like I'm either lacking some fundamental mathematical knowledge to approach the problem of finding the barycenters of these orbits or I'm missing something very important.
I actually believe there may be some fallacies in my reasoning, especially in the Hamiltonian approach I used, which, even being correct(and I'm not even sure about this) from a purely computational standpoint, feels a bit weird from a physical point of view.
Any suggestion or help will be greatly appreciated