3D Printed Piston | Lower mass = Power

[novaguy]

TL;DR Summary

Less work done to reciprocate the piston. Where does that work go?

This is a piston I had DMLS printed from AlSi10mg - the geometry is derived from generative design using some basic inputs and a starting shape. It's really just an experiment whether a consumer grade design and print can be bolted in and work for a time.

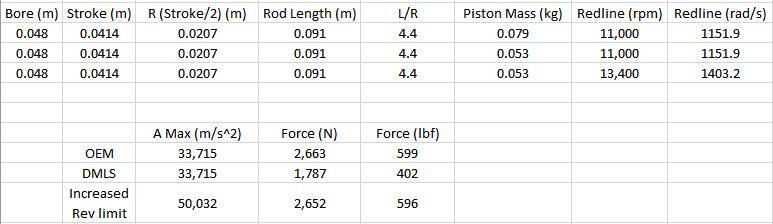
After machining, it is predicted to weigh ~50 grams vs the OEM 79 grams (1970's Honda XR75). The question is, will this lighter piston result in a small power increase as less work done by reciprocating the piston? Theoretically, the rate at which work is done will be increased?

With the reduced mass, the redline could be increased slightly due to less inertia load, but besides that? Of course, the engine should be more responsive (quicker to spin up) and with a much smaller skirt area, less friction too.

By my calculations, at maximum piston acceleration (~TDC) @ 11,000 RPM, the inertia forces on the piston are about 33% less.

 

[novaguy]

Ignoring power increase due to higher RPM capability, just purely the reduced work on the piston; Here's my line of thinking and correct me if I'm wrong:

F = ma
The force from combustion pressure is not changing. The reduced piston mass will increase the acceleration of the piston.

a = dv/dt
The increased acceleration means it will hit higher velocities along the stroke.

P = fv
If the combustion force remains the same and the piston velocity increases, Power should also increase?

 

[berkeman]

Welcome to PF.

I don't know about your power increase question (or the higher RPM capability), but won't it cause issues with the smoothness of the engine? What is the flywheel weight and MoI for the stock piston weight?

 

[novaguy]

Welcome to PF.

I don't know about your power increase question (or the higher RPM capability), but won't it cause issues with the smoothness of the engine? What is the flywheel weight and MoI for the stock piston weight?

Thanks!

It's a possibility that the engine will run rougher - the crank counterweights won't be tuned for the reduced mass pistons. No idea about the flywheel weight.

 

[novaguy]

With lower piston mass, less work has to be done. At 11,000 rpm the piston is accelerating to and from a stop 22,000 times a minute! I imagine this must have some theoretical effect.

If less work is done to move the piston, does the crankshaft and flywheel accelerate faster, increasing the rate of work done (power)?

 

[Baluncore]

It's a possibility that the engine will run rougher - the crank counterweights won't be tuned for the reduced mass pistons.

That is correct. Imbalance becomes a major problem.

A lower weight piston will accelerate faster, but will have no more power.

By reducing the crank counterweight to balance the lighter piston, you can double the acceleration advantage, and get a motor that is balanced.

 

[jrmichler]

At high rates of vehicle acceleration in the lowest gears, a portion of the power is used to accelerate the engine rotating mass. Reducing engine rotating mass will increase the power to the vehicle when accelerating in the lower gears. That's why racers want light weight flywheels. The total power will stay the same, so there will be no change in the top speed.

There is a tradeoff. Reducing rotating mass too much causes other problems. That's why the manufacturer has a flywheel of a certain size on that engine in the first place. Engine manufacturers would just love to reduce cost by eliminating flywheels completely.

With the reduced mass, the redline could be increased slightly due to less inertia load, but besides that? Of course, the engine should be more responsive (quicker to spin up) and with a much smaller skirt area, less friction too.

Yes, less inertia allows increased redline if the limiter is stress in the piston / connecting rod / crankshaft system. If the limiter is valve float, no. And yes to reduced friction from reduced skirt area.

 

[novaguy]

A lower weight piston will accelerate faster, but will have no more power.

Lower piston mass means it takes less force to accelerate. F=ma

Less force over the course of the engine stroke means less work wasted W=fd

Shouldn't this equate to more work output from the crank and flywheel?

 

[novaguy]

At high rates of vehicle acceleration in the lowest gears, a portion of the power is used to accelerate the engine rotating mass. Reducing engine rotating mass will increase the power to the vehicle when accelerating in the lower gears. That's why racers want light weight flywheels. The total power will stay the same, so there will be no change in the top speed.

There is a tradeoff. Reducing rotating mass too much causes other problems. That's why the manufacturer has a flywheel of a certain size on that engine in the first place. Engine manufacturers would just love to reduce cost by eliminating flywheels completely. Yes, less inertia allows increased redline if the limiter is stress in the piston / connecting rod / crankshaft system. If the limiter is valve float, no. And yes to reduced friction from reduced skirt area.

The lower piston reciprocating mass means the connecting rod and crankshaft do less work to propel the piston. With less energy being lost to moving the piston, doesn't that mean the crank and flywheel can release energy faster?

Rate of work done = power

 

[Baluncore]

Lower piston mass means it takes less force to accelerate. F=ma

Less force over the course of the engine stroke means less work wasted W=fd

Shouldn't this equate to more work output from the crank and flywheel?

Not when the engine is developing power at a steady RPM.

The piston and its counterweight are a circulating mass with circulating kinetic energy. The forces are balanced. It is only during acceleration that energy is needed to accelerate the piston and counterweight.

If the engine is not balanced, some circulating energy will be wasted as it radiates vibration through the engine and frame.

 

[jack action]

When at a constant RPM, it is true that the piston will accelerate (from the end to the middle of the cylinder) but it will also decelerate equally (from the middle of the cylinder to the end). But the average acceleration will be zero - otherwise, the RPM wouldn't be constant.

The acceleration of the piston is defined by the RPM and the crank-rod geometry. The forces and masses are irrelevant.

Having a smaller mass will not increase power; the power input is defined by the combustion force and the rate at which it occurs (i.e. the RPM of the engine). The force acting on the piston being the same, the RPM being the same, thus the power is also the same. The only thing a smaller mass will do is give a higher acceleration/deceleration if the resistance force (for example, the aerodynamic drag acting on a vehicle) does not balance out the forces acting on the pistons.

Even though it requires energy to accelerate a mass, it is given back when it decelerates. So the net energy required by acceleration is usually zero. Inertia is related to kinetic energy which can be used as a storage mechanism, like potential energy or spring potential energy.

 

[novaguy]

Having a smaller mass will not increase power; the power input is defined by the combustion force and the rate at which it occurs (i.e. the RPM of the engine). The force acting on the piston being the same, the RPM being the same, thus the power is also the same. The only thing a smaller mass will do is give a higher acceleration/deceleration if the resistance force (for example, the aerodynamic drag acting on a vehicle) does not balance out the forces acting on the pistons.

The combustion pressure (and power created from it) is not increasing of course, that power created is the same regardless of piston mass.

The power that is no longer being "robbed" to move the piston is what I'm wondering about. In my calculations, the power used to move the piston mass goes from 4.5 hp to ~3 hp over the course of 1 engine revolution.

With less power used, that all is lost somewhere? With the same power being harnessed from gas combustion...

 

[novaguy]

At steady state RPM the engine speed isn't changing so the angular acceleration is zero, but the piston is changing speed? Maybe I'm wrong

 

[Baluncore]

At steady state RPM the engine speed isn't changing so the angular acceleration is zero, but the piston is changing speed? Maybe I'm wrong

The piston and counterweight are both changing speed, but in opposite directions, so they cancel. The energy and the forces are balanced. No extra energy is needed to keep the motor spinning.

 

[jack action]

The power that is no longer being "robbed" to move the piston is what I'm wondering about. In my calculations, the power used to move the piston mass goes from 4.5 hp to ~3 hp over the course of 1 engine revolution.

[...]

View attachment 319690

With all due respect, these are the worst calculations ever done. It's just a bunch of meaningless numbers thrown around.

As I said previously, the mean piston acceleration is zero when at constant speed. The number you calculated means "the mean piston speed increases by 15.2 m/s every 0.0055 s". It is not. It stays at 15.2 m/s all the time, thus "the mean piston speed increases by 0 m/s every second", therefore the mean piston acceleration is 0 m/s².

Again, the mean force acting on the piston is dictated by the gases pushing on it. It doesn't change while "going through the piston". If on the other side of the piston there is an equal and opposite force, the piston speed stays the same. If it is different, the piston will accelerate or decelerate. The acceleration will be $a_{piston} = \frac{F_{gases} - F_{opposite}}{m_{piston}}$.

That being said, the instantaneous piston acceleration of a slider-crank mechanism is defined by simple geometry. From this link:

Note that this is true even if there is nothing pushing on the piston or driving the crank. How is that possible? It is like a pendulum: When the crank pushes on the piston it wants to slow down - thus losing energy - but when the piston pushes on the crank during the other half of the revolution it regains it all. All it needs is the initial energy input to start the motion, like when you lift a pendulum to initiate the swinging motion.

 

[novaguy]

With all due respect, these are the worst calculations ever done. It's just a bunch of meaningless numbers thrown around.

Surely there must be worse somewhere in history - it should've been obvious the acceleration of a mean speed is ZERO but not when I cobbled that together. You don't have to be a da(t)/dt about it lol.

So, the answer I am seeing so far is:

With lower piston mass, less energy is required from the crankshaft to accelerate the piston, but the piston also returns less energy to it at the other end of the stroke. Therefore, the energy increase is net-zero.

Again, the mean force acting on the piston is dictated by the gases pushing on it. It doesn't change while "going through the piston". If on the other side of the piston there is an equal and opposite force, the piston speed stays the same. If it is different, the piston will accelerate or decelerate. The acceleration will be $a_{piston} = \frac{F_{gases} - F_{opposite}}{m_{piston}}$.

Theoretically, with less mass, the piston will have increased acceleration from the same combustion force (with opposing forces being equal; friction forces, crankcase pressure, etc).

Is there some measurable or calculable result of that increased piston acceleration? Is it just increased crank angular velocity?

 

[jack action]

Is there some measurable or calculable result of that increased piston acceleration? Is it just increased crank angular velocity?

Let me illustrate the phenomena at hand.

Imagine you have a cube that has a mass of 1000 kg and on it there is another cube with a mass of 0.1 kg. If you push the big cube, you will accelerate both the big cube and the little cube, so the mass $m$ in $F=ma$ will be 1000.1 kg and the acceleration $a$ will be the same for both cubes. If you reduce the mass of the little cube by 50% the only difference will be that the total mass is now 1000.05 kg.

If your piston is in a car that is accelerated with the piston, you have to consider the total inertia, not just the masses alone but also the rotational inertia. How quicker the piston will accelerate depends on how quicker the powertrain, the wheels, and the whole car will accelerate as well. You will be able to define a new equation $F=m_e a$ where $m_e$ is the equivalent mass of the vehicle which is, of course, larger than its true mass. For example, accelerating typical wheels alone on a car reduces the acceleration by about 4 % ($m_e = 1.04 m$). If you would reduce the rotational inertia of the wheels by half, then the acceleration would only be reduced by 2% ($m_e = 1.02 m$).

All the mechanical components are linked together and so are their accelerations (linear or rotational). To find out how to calculate them, see this link.

 

[novaguy]

I should've mentioned from the outset that this piston will be run in a test stand. It will be compared directly with the stock piston in this setup.

In this case the engine won't be under load so drivetrain inertia, drag force, rolling resistance are not factors. Purely looking at the engine as an isolated system, with the flywheel being the output.

In a vehicle, piston mass would have nearly negligible effect on vehicle performance. In engine parameters, it would have a more pronounced effect.

 

[berkeman]

I should've mentioned from the outset that this piston will be run in a test stand. It will be compared directly with the stock piston in this setup.

Were you going to match the counterweights to the piston mass? Or will you just monitor the vibration of the engine with the two different pistons...?

 

[novaguy]

Were you going to match the counterweights to the piston mass? Or will you just monitor the vibration of the engine with the two different pistons...?

It's really just an experiment to see if a generative designed (consumer grade software) piston can be printed without proprietary alloys (unlike Porsche/Mahle who have done this exact thing in the GT2 RS) and work for a "while".

No modifications will be done besides the piston swap. I expected to see a change in the angular acceleration in the flywheel. It was just hard for me to imagine less work being done on the piston and not seeing some effect.

 

[jack action]

I should've mentioned from the outset that this piston will be run in a test stand. It will be compared directly with the stock piston in this setup.

In this case the engine won't be under load so drivetrain inertia, drag force, rolling resistance are not factors. Purely looking at the engine as an isolated system, with the flywheel being the output.

It still follows the same idea: the acceleration of the piston is linked to the accelerations of the connecting rod, crank, and any other component connected to them. Their combined inertia defined their accelerations.

 

[novaguy]

Can someone tell me if this is wrong mathematically?

The equivalent mass of the reciprocating components M_REC (piston and some proportion of the connecting rod) will be reduced by a small amount, due to the piston mass being 33% less.

F_I=M_REC*A_REC

The Inertial Force, F_I will DECREASE with a lighter piston.

Because the Inertial force F_I OPPOSES the force due to combustion F_G, there is a larger positive total force in the direction of F_G. The total downwards force propelling the piston and crankshaft has less force resisting it. More of the combustion pressure is available to drive the crank instead of accelerating a heavier piston. This is not much different than increase power output due to thinner, low tension, coated piston rings.

With more force reaching the crank, this in turn will then create increased total torque by some small amount.

Could this be seen as an increase in efficiency? Work*Efficiency = Work_OUTPUT

 

[jack action]

If you ever find some mathematical equations that seem to demonstrate there will be an increase in efficiency while modifying the mass, then your equations are wrong.

This is not much different than increase power output due to thinner, low tension, coated piston rings.

Oh yes, it is much different. The thinner, low-tension, coated piston rings will create less friction. Friction is energy going away in heat. It cannot be recovered. Inertia is energy stored while gaining speed. When it will slow down, the energy will get back into the system; 100% of it, with no losses whatsoever.

Reducing mass may reduce the normal forces between the components, leading to fewer friction losses. That is the only way you can explore the higher efficiency of your engine.

Let me give you another example to try and show you how you err in your way of thinking:

In a vertical cylinder, the piston mass must go up against gravity, which represents a potential energy loss of $mgh$, where $h$ is the stroke length. Therefore, if I set the cylinder horizontally, the engine will be more efficient because I won't have this loss anymore.

What is wrong with that hypothesis? Well, I ignored that when the piston will go back down, it will also give me back an energy input equivalent to $mgh$ as well. It doesn't matter what the mass is, whatever it takes, it gives back. You are doing the same with kinetic energy instead of potential energy. You have to look at the whole cycle, not just when the gases push on the piston.

 

[Baluncore]

The equivalent mass of the reciprocating components MREC (piston and some proportion of the connecting rod) will be reduced by a small amount, due to the piston mass being 33% less.

Have you forgotten that the main bearing forces will increase due to the unbalance? Main bearing friction losses will therefore increase. The unbalanced forces will radiate vibration energy from the main bearings, through the engine mounts, to the vehicle.

When it comes to energy losses and efficiency, where you model the discrete piston mass, you must also model the discrete counterbalance mass, and the out of balance forces. If you do not do that, you are cherry-picking the gains while ignoring the losses, resulting in a false claim.

 

[novaguy]

I went ahead and plotted these using the actual engine geometry and an assumed gas pressure of 300 psi.

Torque due to reciprocating inertia (piston and con-rod):

Keep in mind, a realistic plot of combustion would be phase shifted and have a sharper peak. However, this does show the contribution of lower inertia on the RATE that the torque is produced.

Total Torque = Inertia Torque + Torque Due to Combustion (the gas pressure is equal for both pistons obviously):

"Given the exact same combustion chamber conditions (this is a huge, glaring condition which is highly unlikely in the real world) making the rotating assembly lighter yields a direct increase in shaft power. This gain, in the real world, is going to be very small - small enough that depending on what specific dyno technology is in use, it's very likely to be impossible to measure consistently- but it's there.

For a particular combustion chamber configuration operating at 100% load, the amount of energy available due to each individual combustion event is fixed. If you start at idle RPM and accelerate under any load, the piston velocity on the compression and expansion strokes are going to be different; the energy to create that difference in velocity comes directly from the fuel being consumed. If the piston is lighter, creating that velocity difference takes less fuel.

If you're operating at 100% load, you are still getting the exact same amount of power extracted from each combustion event - but less of that power is being consumed by accelerating rotating components, and more of it is making it to the output shaft and into the load being accelerated.

The difference might become large enough to become measurable if you were to spend big dollars to lighten every moving component; you'd create other problems (ie, NVH) along the way."

 

[jack action]

Total Torque = Inertia Torque + Torque Due to Combustion

No. Total Torque = Inertia Torque = Torque due to Combustion - Resistive Torque

Imagine that on the other side of the piston, you have an equal and opposite force going against the combustion force. What is the "Inertia Torque"? Zero. The piston doesn't accelerate or decelerate, that's it. If there is no opposite force then "Inertia Torque = Torque due to Combustion", i.e. maximum possible acceleration.

making the rotating assembly lighter yields a direct increase in shaft power.

No. To be exact, the shaft power depends on the resistive torque and shaft RPM. The input power (from combustion) is the same no matter the inertia of the assembly. A lighter assembly with no resistive torque will only give a greater acceleration.

If the piston is lighter, creating that velocity difference takes less fuel.

No. Even if the piston is lighter, the same quantity of fuel is consumed. But the acceleration will be greater.

but less of that power is being consumed by accelerating rotating components, and more of it is making it to the output shaft and into the load being accelerated.

No. The power will be "consumed" by the resistive power. Whatever is left will be used to accelerate the rotating components. The lighter they are, the greater the acceleration. If the resistive power is equal to the input power, then the rotating components will not accelerate.

Whatever energy coming from the combustion that is not "consumed" by the resistive power is stored in kinetic energy. The energy will be given back upon deceleration.

 

[gmax137]

The energy will be given back upon deceleration...

... at the bottom of the power stroke, right?

 

[A.T.]

So, the answer I am seeing so far is:

With lower piston mass, less energy is required from the crankshaft to accelerate the piston, but the piston also returns less energy to it at the other end of the stroke. Therefore, the energy increase is net-zero.

In simple terms: Energy that you put into acceleration is not wasted, but stored as KE. Wasting of energy happens as: friction, non-elastic deformation and in the combustion itself.

So reducing piston mass will not automatically reduce energy waste. It might even increase it, if the parameters change such that the above mechanisms are affected.

 

[jack action]

... at the bottom of the power stroke, right?

If the entire engine assembly is decelerating, it will give back the energy during the whole deceleration period. The decelerating crankshaft has no cyclic component.

 

[novaguy]

Can we agree that lower piston mass will reduce the torque due to inertia?

Can we also agree that the torque resulting from gas expansion is equal for each engine (one with a lighter piston, the other stock)?

And that the total torque generated (not including resistive torques for simplicity) is the sum of these torques?

It seems that the effect of lower reciprocating mass is an increase in the rate of torque. Can anyone confirm or refute this mathematically? Not with conjecture

 

[gmax137]

this journal or whatever you're quoting from looks interesting but honestly the .xyz in the address makes me leery of going there.

 

[novaguy]

Nothing revolutionary but gave some nice equations of motion to plug into with my engine geometry/mass.

Attached is a PDF copy of the paper:

Hailemariam Nigus. Kinematics and Load Formulation of Engine Crank Mechanism. Mechanics, Materials Science & Engineering Journal, 2015, ff10.13140/RG.2.1.3257.1928ff. ffhal-01305936f

 

[jack action]

Can we agree that lower piston mass will reduce the torque due to inertia?

No. If you look carefully, the average torque is zero. Reducing the mass will only reduce the peak values (both positive and negative). Once again, whatever it takes, it gives back; and it takes only one revolution to do so.

And that the total torque generated (not including resistive torques for simplicity) is the sum of these torques?

First, your source considers the entire cycle, i.e 2 revolutions, but you consider only half a revolution. Try redoing your math over the entire cycle and calculate the average torque over the cycle. You will see that nothing changed because the average inertial torque is zero.

Second, these equations assume constant RPM. The model assumes that the torque due to combustion is completely transferred to do work somewhere else. If it wasn't, or the resistive torque would be at least lower than the "torque" coming from the combustion, then this torque difference would accelerate the piston-crank assembly. If it was greater, it would decelerate it.

 

[novaguy]

So, I decided to ask ChatGPT what it thought about the subject

Here is probably the real mechanism behind it, which explains my thinking: lower piston mass can increase the mean effective pressure of the engine.

Reciprocating Inertia: Reducing the mass of the pistons can decrease the reciprocating inertia of the pistons, which means the pistons can accelerate and decelerate more quickly. This allows for a more rapid combustion process and an improvement in the MEP.

Combustion Duration: A reduction in piston mass can also decrease the combustion duration. As combustion duration is reduced, the pressure inside the cylinder increases, resulting in an improvement in the MEP.

I also just asked, "studies done on piston mass". Results? INCREASES IN POWER.

 

[jack action]

which means the pistons can accelerate and decelerate more quickly. This allows for a more rapid combustion process and an improvement in the MEP.

Combustion Duration: A reduction in piston mass can also decrease the combustion duration. As combustion duration is reduced, the pressure inside the cylinder increases, resulting in an improvement in the MEP.

This is complete nonsense. We already determined that the piston acceleration depends only on the RPM and stroke of the engine; the average over a cycle always being zero (at constant RPM).

The only way to reduce the combustion duration (in crank angle) is to reduce the piston speed at TDC. A lower acceleration will achieve that, which only depends on a shorter stroke and/or lower RPM in a traditional engine. The combustion time will remain more or less the same no matter the piston speed. Thus the flame front will have to "chase" the piston at high RPM, getting further away from the ideal constant-volume combustion of the Otto cycle (i.e less efficient). This is the main reason why mean piston speeds higher than 30 m/s are never achieved.

I also just asked, "studies done on piston mass". Results? INCREASES IN POWER.

What is said there is about lowering friction force, and vibrations which can all lead to more power. You already mentioned the friction in the OP:

and with a much smaller skirt area, less friction too.

And the energy losses due to vibrations were also already mentioned:

Main bearing friction losses will therefore increase. The unbalanced forces will radiate vibration energy from the main bearings, through the engine mounts, to the vehicle.

ChatGPT is not a valid source of information. Stop looking for things you want to hear and embrace the already-established science. Basically, all you have to do is a Free Body Diagram (FBD) to answer your question:

will this lighter piston result in a small power increase as less work done by reciprocating the piston?

(The answer should be "no".)