3rd Law: Weight vs Tension (picture)

[merzperson]

1. In case a in the figure block A is accelerated across a frictionless table by a hanging a 10N weight (1.02kg). In case b, block A is accelerated across a frictionless table by a steady 10N tension in the string. The string is massless, and the pulley is massless and frictionless.

Is A's acceleration in case b greater than, less than, or equal to its acceleration in case a?

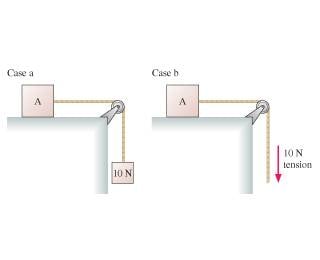
3. I just don't see how a 10N weight differs from a constant 10N downward force on the rope. How is it that the acceleration of block A in case b is greater than in case a? I assume there is some kind of difference because in case a we are comparing two objects and in case b we just calculate the net force on block A, but I can't figure out how to do this.

 

[rl.bhat]

If T is the tension in the rope, in the first case T> 10 N. Where as in the second case T = 10 N. There fore the acceleration in case a is smaller than b.

 

[merzperson]

Your reply implies that as the Tension of the rope increases, the acceleration of block A decreases. This is the exact opposite of what I would expect. Explain?

Also, could you please explain to me how the Tension in case a is greater than 10N?

Thank you.

 

[rl.bhat]

In the first case
mg - T = 10N/g*a, where a is the common acceleration hanging weight and block A.
Similarly
T = mA*a.
In the second case T itself is 10 N.

 

[merzperson]

Thank you very much for your replies. However, I am still having trouble.

I don't understand where you got the equation:
mg - T = 10N/g*a

Or for that matter the other equation. Is mA the mass of block A?

Now I do believe I understand why the tension in case a is not 10N; since the blocks are in motion, the 10N block will not have the effect of 10N. However, I do not know how to tell whether the tension will be greater than or less than 10N, and I haven't a clue how to calculate the tension. Any help with this would be greatly appreciated.

 

[rl.bhat]

Acceleration of the hanging mass is less than g, because it is not falling freely.
So its acceleration is given by the equation
mg - T = ma ------(1), where m is the mass of the hanging block.
Acceleration of the block is given by
T = mA*a ----(2), where mA is the mass ob block A.
Hanging block and block A must move with the same acceleration, because they are connected by a single rope. The common acceleration can be found by solving eq.1 and 2. It comes out to be
a = mg/(m + mA). = 10N/(m + mA)
In the second case acceleration of the block A is
a' = 10N/mA. Now compare the accelerations.