4.1.26 graph of velocity over acceleration graph

[karush]

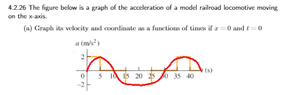
View attachment 9254

ok not finding this easy but the red is mine drawn over the given book graph

also want to convert the whole thing to tikx graph

 

[skeeter]

ok not finding this easy but the red is mine drawn over the given book graph

also want to convert the whole thing to tikx graph

Is the problem's given acceleration graph the piece-wise linear graph in yellow?

Why the graph in red? What's its purpose?

 

[karush]

yes only the red in mine

we are asked to plot velocity(red) over the given graph of acceleration

 

[skeeter]

for the given piece-wise linear acceleration graph in yellow, the velocity graph is as shown ...

 

[I like Serena]

ok not finding this easy but the red is mine drawn over the given book graph

also want to convert the whole thing to tikx graph

We can do for instance:
\begin{tikzpicture}[xscale=.3, >=stealth]
\draw[ystep=0.5,help lines] (0,-2.5) grid (45,2.5);
\draw[->] (-2,0) -- (47,0) node

{(s)};
\draw[->] (0,-2.4) -- (0,2.9) node[above] {$a$ (m/s$^2$)};
\draw
foreach \i in {5,10,...,45} { (\i,0.1) -- (\i,-0.1) node[below] {$\i$} }
foreach \i in {-2,2} { (0.3,\i) -- (-0.3,\i) node

{$\i$} }
(0,0) node[below left] {$0$};
\draw[red, ultra thick]
(5,2) parabola (0,0)
(5,2) parabola (10,0)
(15,-2) parabola (10,0)
(15,-2) -- (25,-2)
(25,-2) parabola (30,0)
(35,2) parabola (30,0)
(35,2) -- (40,2)
(40,2) parabola (45,0);
\end{tikzpicture}

I guess we still need to add the velocity graph.
For the section up to 10 seconds, we have the parabola given by:
$$a(t) = 2 - \frac{2}{25}(t-5)^2 = -\frac{2}{25}t^2+\frac 45 t$$
Integrate it, to find:
$$v(t) = \int_0^t a(t)\,dt = \int_0^t \left[-\frac{2}{25}t^2+\frac 45 t\right]dt
= \left[-\frac{2}{3\cdot 25}t^3 + \frac 25 t^2\right]_0^t = -\frac{2}{75}t^3 + \frac 25 t^2$$

Putting it in a graph, we get:
\begin{tikzpicture}[xscale=.3, yscale=.3, >=stealth]
\draw[help lines] (0,-2.5) grid (45,15);
\draw[->] (-2,0) -- (47,0) node

{(s)};
\draw[->] (0,-2.4) -- (0,15.9) node[above] {$v$ (m/s)};
\draw
foreach \i in {5,10,...,45} { (\i,0.3) -- (\i,-0.3) node[below] {$\i$} }
foreach \i in {-2,5,10,15} { (0.3,\i) -- (-0.3,\i) node

{$\i$} }
(0,0) node[below left] {$0$};
\draw[cyan, ultra thick] plot[domain=0:10, variable=\t] (\t, {-(2/75)*\t^3 + (2/5)*\t^2 });
\end{tikzpicture}

Repeat to find the later sections...
And integrate again to find the x graph...​