- #1
InigoMontoya
- 2
- 0
Hi,
I'm doing a project for math class on Fermat's Last Theorem, and the first thing I wanted to know when I learned what the theorem was, was how a3+b3 = c3 would look in relation to the way a2+b2 = c2 is often depicted. That is, I wanted to know if there was a way to show Fermat's equation to the 3rd power (with a, b, and c as real numbers, not integers, obviously) in a way similar to this:
http://www.clascalc.com/Images/pythagorean-theorem-1.gif
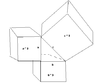
What I came up with last night is depicted in the attached image at the bottom of this post (sorry, I did it quickly in MS paint.. but you get the idea, I think).
What I want to know now is, is my diagram incorrect? Am I wrong in assuming that the cube root of a3+b3 is equal to c when c is the hypotenuse of a right-angled triangle? In other words, sure, you can build three cubes off the sides of a two-dimensional triangle, and you can also measure the sides of that triangle and plug two of the measurements into the equation a3+b3 = c3, but the result given in the equation will not be equal to the measurement you took of the third side?
Does anyone know whether this is true or false? And why? I realize I probably haven't done an excellent job of explaining myself, but I tried my best. I can't seem to find any answers on Google, and I'm having trouble figuring it out for myself - I think I'm just a tiny bit (no sarcasm) out of my depth in this topic (it's meant to be an enrichment project, after all). I did build three cubes out of bristol board today based on an equation I did where 83+83 = c3 (c = 10.079...), but when I tried to put them together as a right-angled triangle, the 'c' cube, or hypotenuse, was too short. It could have just been an error in precision on my part, or it could be an error in the mathematical reasoning. I would be extremely grateful if someone could let me know which one it was.
Thanks!
I'm doing a project for math class on Fermat's Last Theorem, and the first thing I wanted to know when I learned what the theorem was, was how a3+b3 = c3 would look in relation to the way a2+b2 = c2 is often depicted. That is, I wanted to know if there was a way to show Fermat's equation to the 3rd power (with a, b, and c as real numbers, not integers, obviously) in a way similar to this:
http://www.clascalc.com/Images/pythagorean-theorem-1.gif
What I came up with last night is depicted in the attached image at the bottom of this post (sorry, I did it quickly in MS paint.. but you get the idea, I think).
What I want to know now is, is my diagram incorrect? Am I wrong in assuming that the cube root of a3+b3 is equal to c when c is the hypotenuse of a right-angled triangle? In other words, sure, you can build three cubes off the sides of a two-dimensional triangle, and you can also measure the sides of that triangle and plug two of the measurements into the equation a3+b3 = c3, but the result given in the equation will not be equal to the measurement you took of the third side?
Does anyone know whether this is true or false? And why? I realize I probably haven't done an excellent job of explaining myself, but I tried my best. I can't seem to find any answers on Google, and I'm having trouble figuring it out for myself - I think I'm just a tiny bit (no sarcasm) out of my depth in this topic (it's meant to be an enrichment project, after all). I did build three cubes out of bristol board today based on an equation I did where 83+83 = c3 (c = 10.079...), but when I tried to put them together as a right-angled triangle, the 'c' cube, or hypotenuse, was too short. It could have just been an error in precision on my part, or it could be an error in the mathematical reasoning. I would be extremely grateful if someone could let me know which one it was.
Thanks!
Attachments
Last edited by a moderator: