A banked roadway with static friction

[shawli]

Homework Statement

A car rounds a banked curve. The radius of curvature of the road is R, the banking angle is θ, and the coefficient of static friction is μ.

a) Determine the range of speeds the car can have without slipping up or down the road.

Homework Equations

Newton's second law, as well as centripetal acceleration.

The Attempt at a Solution

I'm trying to conceptualize this problem. I saw a similar example with a banked road, except it didn't involve friction.

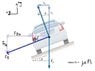
I've attached a picture of what I think the FBD of the car should look like.
My procedure involved a net forces equation in the y-direction and a net forces equation in the x-direction (which is also the "radial" direction, right?).

Fy=0
0 = n*sinθ - mg

Fx= m*a
m*a = n*sinθ + Fs*cosθ
m*v²/r = n*sinθ + μ*n*cosθ

I then isolated both equations for "n", then equated the two resulting expressions to each other to solve for v. I don't seem to be getting the correct expression in the end... Any suggestions on what I might be doing wrong? I suspect it has something to do with the way I've looked at the force of static friction, although I don't know for sure. Maybe I'm missing something conceptual...

Help would be greatly appreciated :)

Edited: Oh - I'm also unsure about the "ranges" aspect of this question. What's the difference between "slipping up" and "slipping down"? In my FBD, I don't seem to have a force that would result in "slipping up" since all point inwards/towards centre of the circle. I can only imagine "slipping down" to occur...

 

[ehild]

The force of friction has both x and y components.

The force of friction can act both up and down along the road, to prevent the car from slipping down or up, respectively.

ehild

 

[shawli]

Whoops, thank you. Changing the equations...

Fy=0
0 = n*sinθ - mg - Fs*sinθ
0 = n*sinθ - mg - μ*n*sinθ

Fx= m*a
m*a = n*sinθ + Fs*cosθ
m*v2/r = n*sinθ + μ*n*cosθSo this set-up is correct for the net forces?

 

[ehild]

Fy=0
0 = n*sinθ - mg - Fs*sinθ

It has to be cosθ.

ehild

 

[shawli]

Thanks again! I end up with the correct expression for "minimum velocity", but I still don't quite understand what makes the difference between slipping up/slipping down.

In what case would friction be working "up" along the road? I can redraw my FBD to show that but I'm not sure what the car is actually doing in this moment... What force is acting on the car to make it so that friction acts from the opposite side?

 

[ehild]

In what case would friction be working "up" along the road? I can redraw my FBD to show that but I'm not sure what the car is actually doing in this moment... What force is acting on the car to make it so that friction acts from the opposite side?

It is gravity. What happens if the car stops on a icy banked road? What would prevent it to slide down on the sloppy surface ?

It is dangerous to drive to slow as you slide inward. It is dangerous to drive to fast as you slide outward.

ehild