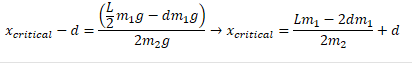A bar suspended by two vertical strings

[jonny997]

Homework Statement

A rigid, uniform, horizontal bar of mass m_1 and length L is supported by two identical massless strings. Both strings are vertical. String A is attached at a distance d<L/2 from the left end of the bar and is connected to the ceiling; string B is attached to the left end of the bar and is connected to the floor. A small block of mass m_2 is supported against gravity by the bar at a distance x from the left end of the bar, as shown in the figure.

Throughout this problem, positive torque is that which spins an object counterclockwise. Use g for the magnitude of the acceleration due to gravity.

Relevant Equations

Net torque = 0

Diagram

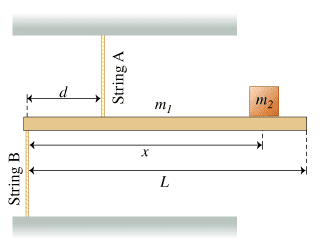
Problem
If the mass of the block is too large and the block is too close to the left end of the bar (near string B) then the horizontal bar may become unstable (i.e., the bar may no longer remain horizontal).
What is the smallest possible value of x such that the bar remains stable (call it x_critical)?

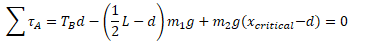
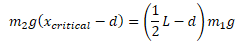
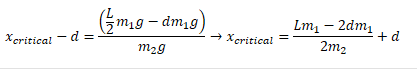
The correct answer turned out to be

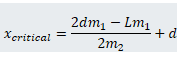
Which is what you get when the torque is negative...

I'm just not 100% how to figure out whether the torque caused by mass 2 should be positive or negative? I assumed it would be to the left of string A and cause positive torque. Can someone help me figure this out?

 

[Steve4Physics]

Welcome to PF @jonny997.

If the system is'critical', which of the following is true:
A) m₂ must be on the right side of string A.
B) m₂ must be on the left side of string A.
C) m₂ could be on either side of string A.
D) There is insufficient information to choose from A, B and C.

Once you've answered, check your original equation.

 

[jonny997]

Hey.

Could it be on either side depending on m₁ and m₂?

 

[haruspex]

View attachment 299792

Check the signs on the torque contributions in your first equation.

 

[jonny997]

Check the signs on the torque contributions in your first equation.

Hey.

I think I've got it... Am I supposed to check how the critical distance varies with m₁ in order to determine the correct signs for the torque caused by mass m₂?

 

[haruspex]

Hey.

I think I've got it... Am I supposed to check how the critical distance varies with m₁ in order to determine the correct signs for the torque caused by mass m₂?

No, you just have to write the equation correctly.

 

[jonny997]

Sorry if i wasn't clear in my first post. That's kinda what I've been struggling with, trying to figure out the correct signs. I just assumed that the m₂ would be to the left of String A but I suppose it could be to the right as well... The question also states that d < L/2 so

would suggest that x gets bigger as the bar gets heavier, which doesn't make sense...
It didnt really occur to me to check that earlier though, I am not sure if there's something I'm missing/not understanding...

 

[jonny997]

No, you just have to write the equation correctly.

Lol yea sorry, I'm just not sure how to figure out what the correct sign is for m₂

 

[haruspex]

Lol yea sorry, I'm just not sure how to figure out what the correct sign is for m₂

x-d is an offset measured which way from string A? I'm not asking which way It will turn out to be since that will depend on the relative magnitudes of d and x; I am asking which way you would be measuring it to use x-d rather than d-x.
Does a downward force exerted that side of A exert a positive or negative torque?

 

[jonny997]

x-d is an offset measured which way from string A? I'm not asking which way It will turn out to be since that will depend on the relative magnitudes of d and x; I am asking which way you would be measuring it to use x-d rather than d-x.
Does a downward force exerted that side of A exert a positive or negative torque?

Oh wait, no I've made a really dumb mistake... The block musr definitely be to the left of string A for the tension in string B to equal 0. I've just got the signs for distance wrong... the way it is right now (x-d) is inverted which is why the direction of the torque is as well... Is that right?

 

[Steve4Physics]

Oh wait, no I've made a really dumb mistake... The block musr definitely be to the left of string A for the tension in string B to equal 0. I've just got the signs for distance wrong... the way it is right now (x-d) is inverted which is why the direction of the torque is as well... Is that right?

Yes. Well done. To make your sign convention work correctly $d-x_{critical}$ must be a positive quantity.

 

[haruspex]

Oh wait, no I've made a really dumb mistake... The block musr definitely be to the left of string A for the tension in string B to equal 0. I've just got the signs for distance wrong... the way it is right now (x-d) is inverted which is why the direction of the torque is as well... Is that right?

Yes, except that the mistake is not a matter of failing to realize it must be to the left of A.
Whichever side it is of A, x-d is the displacement of m2 to the right of A. That is true whether it is positive or negative. So (x-d)m2g is the torque measured clockwise. Hence its contribution to the total torque is -(x-d)m2g.

 

[jonny997]

Yes, except that the mistake is not a matter of failing to realize it must be to the left of A.
Whichever side it is of A, x-d is the displacement of m2 to the right of A. That is true whether it is positive or negative. So (x-d)m2g is the torque measured clockwise. Hence its contribution to the total torque is -(x-d)m2g.

Thanks. It's definitely more intuitive for me to think of the distance as d-x. In this case x-d would be a negative value for m2 to the right of string A, am I right in saying that..? I think that's why I was getting so confused by the signs towards the end...

 

[haruspex]

In this case x-d would be a negative value for m2 to the right of string A, am I right in saying that..?

Yes, and that would drop out of the answer without having to guess it in advance.
That principle applies to most mechanics problems: e.g. you don't have to guess which way a force acts; just suppose it acts one way and write the equations accordingly. If it acts the other way you will get a negative answer.
There may be exceptions, though.

 

[Steve4Physics]

Thanks. It's definitely more intuitive for me to think of the distance as d-x. In this case x-d would be a negative value for m2 to the right of string A, am I right in saying that..? I think that's why I was getting so confused by the signs towards the end...

I think @haruspex ’s approach is more useful/general. It doesn’t require you to know - in advance - where the critical position is. In more complicated problems the critical position may not be clear.

If you follow your sign convention, your original equation (based on the diagram)
$T_{B}d - (\frac 1 2 L – d) m_1g + m_2g(x_{critical} – d) = 0$
should be
$T_{B}d - (\frac 1 2 L – d) m_1g - m_2g(x_{critical} – d) = 0$

You made a simple sign-error (hence @haruspex's comment in Post #6).

 

[jonny997]

Yes, and that would drop out of the answer without having to guess it in advance.
That principle applies to most mechanics problems: e.g. you don't have to guess which way a force acts; just suppose it acts one way and write the equations accordingly. If it acts the other way you will get a negative answer.
There may be exceptions, though.

Ahhh okay, I'll keep that in mind. Thank you!

 

[jonny997]

I think @haruspex ’s approach is more useful/general. It doesn’t require you to know - in advance - where the critical position is. In more complicated problems the critical position may not be clear.

If you follow your sign convention, your original equation (based on the diagram)
$T_{B}d - (\frac 1 2 L – d) m_1g + m_2g(x_{critical} – d) = 0$
should be
$T_{B}d - (\frac 1 2 L – d) m_1g - m_2g(x_{critical} – d) = 0$

You made a simple sign-error (hence @haruspex's comment in Post #6).

Thanks for help haha. I appreciate it