- #1
ThorX89
- 13
- 0
Hi.
I'm curious, how would a charged particle, let's say an electron, move in a simple uniform electric field?
My first guess would be that it would follow Newton's second law of motion and move with a constant acceleration:
[tex]$ \dot{x}=\frac{Eq}{m} $[/tex]
where E is the fields intensity, q the charge, and m it's mass.
However, an accelerated charge should generate electromagnetic waves.
These have energy and so the motion wouldn't accelerate as fast.
I found that the energy radiated by these should be equal to:
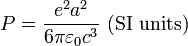
(Larmor formula) for norelativistic speeds.
So I would assume that the work done by the electric field on the charge in a fraction of time:
[tex]$ P_{el} = q\cdot E \cdot \dot{x} $[/tex]
would be used to a) increase the kinetic energy of the particle b) used for the radiation energy:
[tex]\[P_{el}=\frac{d}{dt}(\frac{1}{2}m\dot{x}^2) + P_{rad}\][/tex]
That leads to the differential equation:
[tex]$ A \cdot \dot{x} = m \cdot \dot{x} \cdot \ddot{x} + B \cdot \ddot{x}^2 $[/tex]
where
[tex]$ A=Eq ; B=\frac{{q^2}}{{6\cdot\pi\eps_0\ c^3}} $[/tex]
(just to make it look simpler).
I have now idea how to solve this.
Do you think my reasoning is right? If so, can anybody find a solution?
How is the motion of a charged particle in a uniform electric field truly described?
I'd think this is quite a simple question, but I couldn't find any simple answer to it on the Internet.
I appreciate any help.
I'm curious, how would a charged particle, let's say an electron, move in a simple uniform electric field?
My first guess would be that it would follow Newton's second law of motion and move with a constant acceleration:
[tex]$ \dot{x}=\frac{Eq}{m} $[/tex]
where E is the fields intensity, q the charge, and m it's mass.
However, an accelerated charge should generate electromagnetic waves.
These have energy and so the motion wouldn't accelerate as fast.
I found that the energy radiated by these should be equal to:
(Larmor formula) for norelativistic speeds.
So I would assume that the work done by the electric field on the charge in a fraction of time:
[tex]$ P_{el} = q\cdot E \cdot \dot{x} $[/tex]
would be used to a) increase the kinetic energy of the particle b) used for the radiation energy:
[tex]\[P_{el}=\frac{d}{dt}(\frac{1}{2}m\dot{x}^2) + P_{rad}\][/tex]
That leads to the differential equation:
[tex]$ A \cdot \dot{x} = m \cdot \dot{x} \cdot \ddot{x} + B \cdot \ddot{x}^2 $[/tex]
where
[tex]$ A=Eq ; B=\frac{{q^2}}{{6\cdot\pi\eps_0\ c^3}} $[/tex]
(just to make it look simpler).
I have now idea how to solve this.
Do you think my reasoning is right? If so, can anybody find a solution?
How is the motion of a charged particle in a uniform electric field truly described?
I'd think this is quite a simple question, but I couldn't find any simple answer to it on the Internet.
I appreciate any help.