A circuit involving two non-linear resistances (incandescent lamps)

[Jan Vesely]

Homework Statement

Ok, this is a problem from our textbook and I really do not know how to approach this one, I searched the interned a could not find something similar. I cannot just use Ohm’s Law because the resistor is changing in value. Any help would be appreciated :).

Relevant Equations

U = I * R

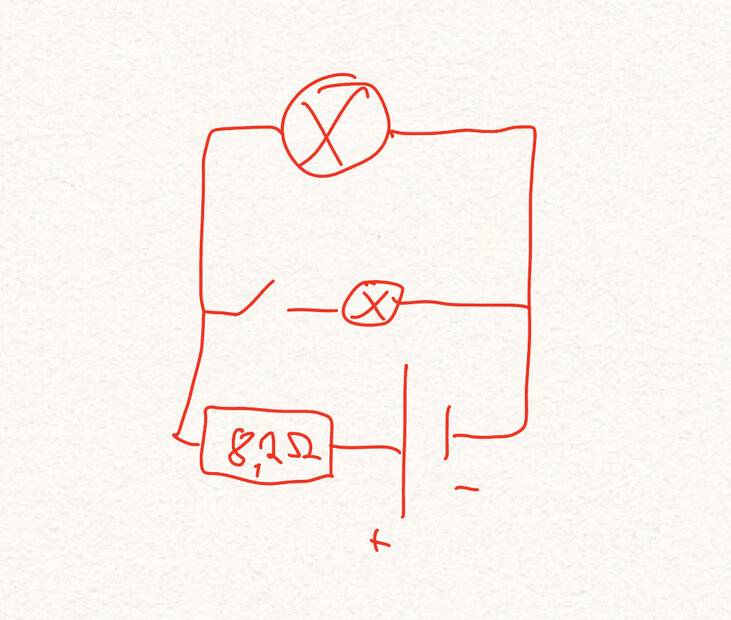
In the circuit, two identical incandescent lamps are connected to a voltage source of voltage U = 6.0 V via an ohmic resistor of magnitude
R= 8.2 are connected to a voltage source of voltage U = 6.0 V.
As electrical components, incandescent lamps do not behave like ohmic resistors. When current flows through a lamp, it heats up and changes its electrical resistance. The table gives the current 1 flowing through an incandescent lamp for the incandescent lamps used, at various voltages U dropped across the lamp.
2.a) Determine the amperage / of the current flowing through the resistor when the switch is open.
2.b) Determine how high the voltage of the battery must be so that a current of the same intensity / flows through the resistor when the switch is closed.
current of the same amperage / flows through the resistor.

V: 0,17	0,67	1,18	1,66	2,33	3,05	3,85	4,73	5,37	6,00
mA: 83	132	175	208	251	290	329	368	395	420

 

[berkeman]

Welcome to PF.

I think the first thing you need to do is put those numbers into an Excel spreadsheet and calculate a 3rd column which is the effective resistance for each row. Then look at how that lamp resistance varies with voltage to plan how you will approach the questions. You may need to interpolate between rows in the end, but it's hard to tell at first...

 

[Jan Vesely]

Welcome to PF.

I think the first thing you need to do is put those numbers into an Excel spreadsheet and calculate a 3rd column which is the effective resistance for each row. Then look at how that lamp resistance varies with voltage to plan how you will approach the questions. You may need to interpolate between rows in the end, but it's hard to tell at first...

I thought about this, if I plot it I can see that it is rapidly increasing. I just don’t know how to calculate the voltage after the first resistor. Thanks for the reply :)

 

[berkeman]

I would still stay with the Excel spreadsheet to calculate the first operating point. After you add the column for the resistance as a function of voltage, maybe make a new table that calculates the resistor voltage divider numbers. Can you give that a try?

BTW, it's best not to attach Excel files since they can contain macros. Instead, take screenshots of your spreadsheet and upload those PDF or JPEG copies.

 

[kuruman]

Questions
1. Am I correct in assuming that the voltages and currents posted are for either bulb when the switched is closed?
2. How do these values line up? You show 10 voltages but only 9 currents.

 

[Jan Vesely]

I would still stay with the Excel spreadsheet to calculate the first operating point. After you add the column for the resistance as a function of voltage, maybe make a new table that calculates the resistor voltage divider numbers. Can you give that a try?

BTW, it's best not to attach Excel files since they can contain macros. Instead, take screenshots of your spreadsheet and upload those PDF or JPEG copies.

I am not the best with Excel..

 

[Jan Vesely]

Questions
1. Am I correct in assuming that the voltages and currents posted are for either bulb when the switched is closed?
2. How do these values line up? You show 10 voltages but only 9 currents.

1: It is for each of the bulbs, not for the whole circuit, so it does not matter whether the switch is opened or not for the table.

2: I added a table

 

[kuruman]

What does the plot in post #6 show? I can guess that the vertical axis is (V/I) but I cannot guess what the horizontal axis is. Please add labels to your axes and repost or edit post #6. Also the first point in that plot is too low. Please check it.

 

[nasu]

You have two equations relating the current through one bulb and the volage across the bulb. One is non-linear (and actually unknown analitically, in general).
The first equation is $$\Delta V =f(i) $$ Here i is the current through one light bulb and $\Delta V$ is the voltage across it. For this relationship you only have the given values of $i$ and $\Delta V$.
The second one depends on the two cases. For the open switch, you have
$$ \Delta V= E-iR$$
In order to solve these two you can plot both of them (the second one is a straight line) and find the point of intersection of the two curves. This will give the actual current and voltage for the circuit.
For this probem the data for the bul is probably made up as it fits almost perfectly a second order polynomial. So you could use the fitting function and the second equation to solve analitically for the current.
For the situation with the switch close you just need to change the second equation accordingly and plot the new line.

 

[DaveE]

This is often solved as a first attempt graphically. Plot on V & I axes the "load line" of the lamps with the data given. Then also plot the source line of the battery plus the resistive drop for each current draw. The solution is where these curves intersect. If that's not good enough, you will need to interpolate a V,I model near the operating point.

Sorry for a terse description, but I have to leave. Others can surely elaborate if needed.

PS: https://en.wikipedia.org/wiki/Load_line_(electronics)#:~:text=In graphical analysis of nonlinear,device by the external circuit.

 

[Mister T]

I am not the best with Excel.

Is there some other graphing software that you have more experience with? I can't make sense of the graph you created with Excel.

 

[DaveE]

I have often solved this sort of problem with a trial and error approach in a simple spreadsheet. It's a crude approach but surprisingly fast with as much accuracy as you like.

If you want mathematical rigour, then you must construct a function to fit your data and solve the resulting KVL/KCL equations. My issue with that is that the exact solution is better than this sort of data usually justifies. It won't be as accurate when one of those lamps is replaced with another that is supposed to be the same.

 

[DaveE]

I think the first thing you need to do is put those numbers into an Excel spreadsheet and calculate a 3rd column which is the effective resistance for each row.

And a 4th column for the necessary offset voltage. The linear model between two data points will have a slope (resistance) and an offset voltage. You'll need both for this approach to linearization.

The locally linear circuit model for the lamp is a battery in series with a resistor. This is just the model for a straight line drawn between the two nearest data points. As the operating point changes, those values change.

 

[BvU]

I am not the best with Excel..

$\qquad$ !​

If financial folks and sociologists can deal with it, anyone can (deal with Excel )

So for 2a you want to read off the current when the V_tot is 6 V.

2b then requires some gymnastics (a.k.a. addition) with the same V_R (because same current) and V_lamp at half that current.
Not too hard...

$\$

 

[Steve4Physics]

The following approach is relatively simple/quick and (I think) hasn’t been suggested yet. For question 2.a) ...

Consider, for example, the data point when the pd across a lamp is 0.67V and the current through it is 0.132A. If this were the operating point, the pd across the resistor would be IR = 0.132*8.2 = 1.0824V. The total pd $U_{tot}$ across the lamp and resistor would be 0.67 + 1.0824 = 1.7524V.

Similarly find $U_{tot}$ for other data points.

Plot total $U_{tot}$ against current.

At the required operating point, $U_{tot}$ equals the supply voltage (6.0V). Just read the current off the graph.

(In fact you probably don’t need a graph; simple linear interpolation might be adequate. And you don’t really need to find $U_{tot}$ for all data points. So the problem can be solved pretty quickly.)