tstl
- 5
- 0
Thread moved from the technical forums to the schoolwork forums
I've a small molecule ABCD made of building blocks A,B,C,D. The molecule can get cleaved at any 'bond' between the building block one bond at a time.
Researchers have compiled probabilities from dissociation studies of large number of molecules( made up of many other building blocks) and the dissociation probs are as follows say:
A:B = 0.1, B:C = 0.7, C:D = 0.3
So, when the bond between A-B breaks, I get a FRAGMENT PAIR with some prob (0.1) plus the molecule ABCD has some prob. 1-0.1 = 0.9 to remain undissociated.
However, as these probs are derived from a large dataset I've to normalize the probabilities so that, the sum of the probabilities of the exhaustive events becomes one for my case.
Hence,
the normalizing constant (k) would follow:
k * ( 0.1 + (1-0.1) + 0.7 + (1- 0.7) + 0.3 + ( 1- 0.3) ) = 1.0
or, k * 3 = 1.0
or, k = 1/3 = 0.33
So. the normalized probs of fragment pairs
p(A, BCD) = 0.1 * 0.33 =0.033
p(AB, CD) = 0.7 * 0.33 = 0.231
p(ABC, D) = 0.3 * 0.33 = 0.099
and the total prob. of ABCD to remain un-fragmented = (1-0.1) *0.33 + (1-0.7) * 0.33 + (1-0.3) *0.33 = 0.297 + 0.099 + 0.231 = 0.627
Am I doing it right?
Thanks
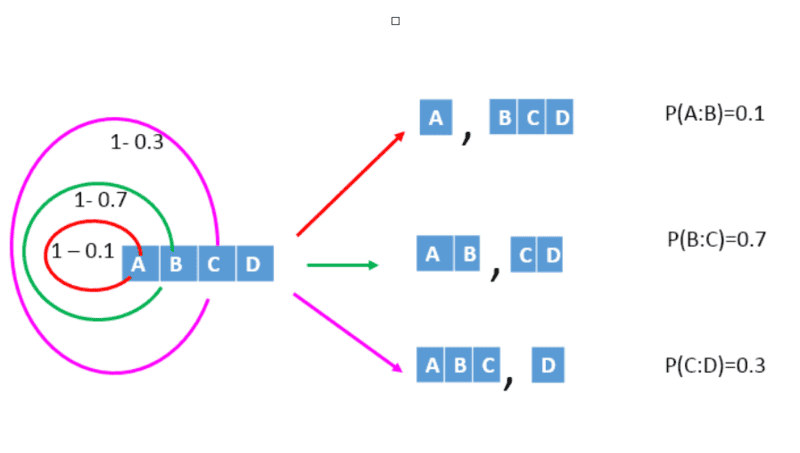
Researchers have compiled probabilities from dissociation studies of large number of molecules( made up of many other building blocks) and the dissociation probs are as follows say:
A:B = 0.1, B:C = 0.7, C:D = 0.3
So, when the bond between A-B breaks, I get a FRAGMENT PAIR with some prob (0.1) plus the molecule ABCD has some prob. 1-0.1 = 0.9 to remain undissociated.
However, as these probs are derived from a large dataset I've to normalize the probabilities so that, the sum of the probabilities of the exhaustive events becomes one for my case.
Hence,
the normalizing constant (k) would follow:
k * ( 0.1 + (1-0.1) + 0.7 + (1- 0.7) + 0.3 + ( 1- 0.3) ) = 1.0
or, k * 3 = 1.0
or, k = 1/3 = 0.33
So. the normalized probs of fragment pairs
p(A, BCD) = 0.1 * 0.33 =0.033
p(AB, CD) = 0.7 * 0.33 = 0.231
p(ABC, D) = 0.3 * 0.33 = 0.099
and the total prob. of ABCD to remain un-fragmented = (1-0.1) *0.33 + (1-0.7) * 0.33 + (1-0.3) *0.33 = 0.297 + 0.099 + 0.231 = 0.627
Am I doing it right?
Thanks