A curved wire rotating in and out of a magnetic field

[Jaccobtw]

Homework Statement

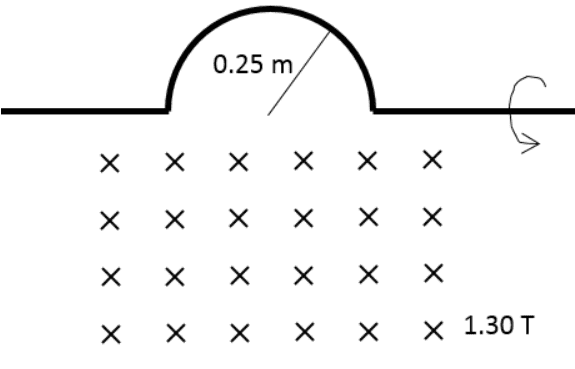
A wire is bent to contain a semi-circular curve of radius 0.25m. It is rotated at 120rev/min as shown into a uniform magnetic field below the wire of 1.30T. What is the maximum emf induced between the left and right sides of the wire in V?

Relevant Equations

$$\Phi =\int_{}^{}B \cdot dA$$
$$\varepsilon = -\frac{d\Phi}{dt}$$

If I'm correct then the maximum change in magnetic flux occurs when the semi circle crosses the point at which it's plane is parallel with the magnetic field and minimal when it crosses the point at which the magnetic flux is maximum ( perpendicular with the field). I'm having trouble writing a function because I'm assuming the magnetic field is located only below the wire and NOT in the semicircle in its up most position. Any ideas? Thank you.

 

[haruspex]

trouble writing a function

It's quite ok to write a function involving a conditional:
f(x)= (expression 1) when x<c
f(x)= (expression 2) when x>c.
The derivative won't exist at exactly c, but it can exist each side of c.

 

[Jaccobtw]

It's quite ok to write a function involving a conditional:
f(x)= (expression 1) when x<c
f(x)= (expression 2) when x>c.
The derivative won't exist at exactly c, but it can exist each side of c.

What exactly is c?

 

[Jaccobtw]

It's quite ok to write a function involving a conditional:
f(x)= (expression 1) when x<c
f(x)= (expression 2) when x>c.
The derivative won't exist at exactly c, but it can exist each side of c.

Ok let's say that the position the loop is in in the picture is $\pi/2$. The magnetic field begins at $\pi$ and ends at $2\pi$. When x is less than $\pi$ the magnetic flux is zero. When x is greater than $\pi$ the flux varies depending on the angle with the magnetic field.

 

[haruspex]

Ok let's say that the position the loop is in in the picture is $\pi/2$. The magnetic field begins at $\pi$ and ends at $2\pi$. When x is less than $\pi$ the magnetic flux is zero. When x is greater than $\pi$ the flux varies depending on the angle with the magnetic field.

Right, so what is the flux for $\pi<\theta<2\pi$? What is the emf over that range?

 

[Jaccobtw]

$$\Phi (t) = BAcos(4\pi t) $$
$$ \varepsilon (t) = \frac{d}{dt} BAcos(4\pi t)$$

 

[haruspex]

$$\Phi (t) = BAcos(4\pi t) $$
$$ \varepsilon (t) = \frac{d}{dt} BAcos(4\pi t)$$

So do the differentiation and find the max pdf.

 

[Jaccobtw]

So do the differentiation and find the max pdf.

$$\varepsilon (t) = BA4\pi sin(4\pi t)$$

 

[haruspex]

$$\varepsilon (t) = BA4\pi sin(4\pi t)$$

And the max value of that is?

 

[Delta2]

Notice that the problem asks not for "When" the maximum EMF occurs but what is the maximum emf. You can answer that, either by answering first the "when" or not answering it at all.

 

[Jaccobtw]

And the max value of that is?

At 0.125 seconds. I got it right. Would you have done anything differently?

 

[Delta2]

Not sure but from the shown figure regarding the starting position of the wire and if the magnetic field doesn't fill the whole area, I think at t=0.125sec the wire hasn't yet entered the magnetic field so the EMF is still zero at that time.

EDIT: Anyway the problem asks for the maximum EMF which will be the same, what is the EMF at t=0.125sec(if the magnetic field fill the whole space)?

 

[Jaccobtw]

Not sure but from the shown figure regarding the starting position of the wire and if the magnetic field doesn't fill the whole area, I think at t=0.125sec the wire hasn't yet entered the magnetic field so the EMF is still zero at that time.

EDIT: Anyway the problem asks for the maximum EMF which will be the same, what is the EMF at t=0.125sec(if the magnetic field fill the whole space)?

Then I guess it would be at 0.375 seconds since it would cross the magnetic field at that point and then go into the non field area. I got 1.6 V

 

[Jaccobtw]

Not sure but from the shown figure regarding the starting position of the wire and if the magnetic field doesn't fill the whole area, I think at t=0.125sec the wire hasn't yet entered the magnetic field so the EMF is still zero at that time.

EDIT: Anyway the problem asks for the maximum EMF which will be the same, what is the EMF at t=0.125sec(if the magnetic field fill the whole space)?

If the loop starts at position $\pi/2$ and moves a quarter rotation in an 8th of a second, wouldn't 0.125 seconds be the point at which it begins to enter the magnetic field?

 

[Delta2]

Then I guess it would be at 0.375 seconds since it would cross the magnetic field at that point and then go into the non field area. I got 1.6 V

Yes I think those are the correct answers according to my opinion

If the loop starts at position $\pi/2$ and moves a quarter rotation in an 8th of a second, wouldn't 0.125 seconds be the point at which it begins to enter the magnetic field?

Yes, the loop will just start entering the magnetic field area at t=0.125sec but the derivative of the flux doesn't exist for t=0.125sec because the left derivative is zero while the right derivative is 1.6V.

 

[Delta2]

Oh wait, for the same reason the derivative of the flux doesn't exist at t=0.375sec. Hmmm wth is going on here... @haruspex help please?

 

[haruspex]

Oh wait, for the same reason the derivative of the flux doesn't exist at t=0.375sec. Hmmm wth is going on here... @haruspex help please?

It exists for $0.125s<t<0.375s$. Although the supremum value $4AB\pi$ is not achieved, you can get arbitrarily close to it.
Of course, in the real world, field strengths don't have such discontinuities.

 

[Delta2]

Of course, in the real world, field strengths don't have such discontinuities.

They can have discontinuities if there are different mediums (with different permeability-permittivity) but here it is implied that we have only one medium, vacuum.

 

[Orodruin]

They can have discontinuities if there are different mediums (with different permeability-permittivity) but here it is implied that we have only one medium, vacuum.

… or current densities. But it seems weird to have a current density where the wire is being rotated.

Also just to note: The derivative here does exist across the boundary. However, the second derivative is discontinuous.

 

[Delta2]

Also just to note: The derivative here does exist across the boundary. However, the second derivative is discontinuous.

Sorry which derivative exists? The flux derivative doesn't exist (for me at least) as the left derivative (for 0<t<0.125) is 0, while the right derivative is $4\pi BA$.

 

[haruspex]

They can have discontinuities if there are different mediums

In the real world, media do not have exact boundaries. I'm thinking of the atomic scale.

 

[Delta2]

In the real world, media do not have exact boundaries. I'm thinking of the atomic scale.

Hm.. yes i think you are right, media with exact boundaries can happen only in the classical world of the 19th century.