A diamagnetic sphere in a uniform magnetic field

[milkism]

Homework Statement

a) Find the induced surface current density
b) Find the M, B and H-fields

Relevant Equations

See solution.

Problem:

Solution part a)

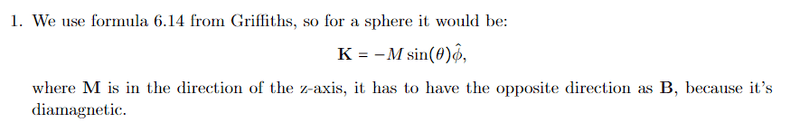
where formula 6.14 is just M x n.

We need to do part b without seperation of variables, I'm quite stuck. Will B just be the magnetic field inside a solenoid? How can I find the other fields.

 

[Charles Link]

See https://www.physicsforums.com/threa...f-homogeneous-dielectric.940015/#post-5943369

The solution is similar for the analogous magnetic problem. There are Legendre methods for solving this, but it can help to start with a simpler approach.

There is $D=\epsilon _o E+P$ and $B=\mu_o H+M$. You need to watch the units on $M$ though when transposing the two, because some books write it as $B=\mu_o H +\mu_o M$.

 

[Charles Link]

One additional input: You really need to compute the resulting magnetization $M$ before you can do part "a" which is to compute the magnetic surface current density.

additional item: to compute the magnetic field $B$ outside the sphere, the most practical way seems to be to use Legendre methods, although I think Griffith's in his E&M book presents an alternative way that also works. See https://www.physicsforums.com/threa...ormly-polarized-cylinder.941830/#post-5956930
The above is for a cylinder, but the method would also work for a sphere.

 

[milkism]

One additional input: You really need to compute the resulting magnetization $M$ before you can do part "a" which is to compute the magnetic surface current density.

additional item: to compute the magnetic field $B$ outside the sphere, the most practical way seems to be to use Legendre methods, although I think Griffith's in his E&M book presents an alternative way that also works. See https://www.physicsforums.com/threa...ormly-polarized-cylinder.941830/#post-5956930
The above is for a cylinder, but the method would also work for a sphere.

We need the external magnetic field to calculate the external H-field? The M-field outside is zero.

 

[Charles Link]

The $E$ and $H$ are corresponding fields when transposing the two. If you can follow how the $E$ is calculated, you then convert it to $H$ with $\mu_o$ in place of $\epsilon_o$, and $M$ in place of $P$.

and yes, for $B_{outside}$, the $M_{outside}=0$ so that $B_{outside}=\mu_o H_{outside}$.

One additional note: You might find this thread on magnetostatics to be good reading: https://www.physicsforums.com/threads/a-magnetostatics-problem-of-interest-2.971045/

and it pays to use units on $M$ where $B=\mu_o H+M$ in doing these problems with comparisons to the electric field, and convert afterwards, if your book uses an $M'$ where $B=\mu_o H+\mu_o M'$.

See https://www.physicsforums.com/threa...iformly-polarized-sphere.877891/#post-5513730 post 7, to get $E_{outside}$. To this you need to add the applied field, but that part is simple. Once you have $E_{outside}$ you can transpose to $H_{outside}$. (The uniform $P$ (or $M$) that you get with an applied field should be a simple matter to compute, using the link of post 2 above with the demagnetizing factor $D=1/3$ for a sphere).

 

[Charles Link]

@milkism Did you get an answer for the $M$ ?

 

[milkism]

@milkism Did you get an answer for the $M$ ?

Luckily we were allowed to use already calculated expressions for the internal- and external magnetic fields. This is what I got:

(The angular velocity is supposed to be bold, but I have dificulty bolding greek symbols. And "with our own given magnetic susceptibility" instead of out.).

 

[Charles Link]

I don't agree completely with your answer. Since this is really not an Introductory Physics problem, let me show you what I got for $B_{inside}$ and $H_{inside}$, etc. The first part I don't agree with that $B_{inside}=(2/3) M$ using units where $B=\mu_o H+M$ and $M=\mu_o \chi H=-\mu_o |\chi| H$, because $H_i=H_a-M/(3 \mu_o)$, so the $H_a$ complicates matters somewhat.

Let me show you how the $H_i$ is obtained from $H_a$, where you really need a $B_a$ with a subscript for the applied $B$, where $B_a=\mu_o H_a$.
$E_i=E_a-P/(3 \epsilon_o)$ using the demagnetizing factor $D=1/3$ for a sphere.
Now $P= P_i=\epsilon_o \chi E_i$ so $E_i=E_a/(1+\frac{\chi}{3})$, so that $H_i=H_a/(1-\frac{|\chi|}{3})$, and $M=-\mu_o |\chi| H_i=-|\chi|B_a/(1-\frac{|\chi|}{3})$, and $B_i=\mu_o(1+\chi )H_i=B_a(1-|\chi|)/(1-\frac{|\chi|}{3})$.

Note: $M=\mu_o \sigma R \omega$, but not every formula works for that solution, because of the $B_a$.

Once we get agreement with the inside, then we'll take a closer look at the outside. Please let me know if you were able to follow the calculations.

 

[milkism]

I don't agree completely with your answer. Since this is really not an Introductory Physics problem, let me show you what I got for $B_{inside}$ and $H_{inside}$, etc. The first part I don't agree with that $B_{inside}=(2/3) M$ using units where $B=\mu_o H+M$ and $M=\mu_o \chi H=-\mu_o |\chi| H$, because $H_i=H_a-M/(3 \mu_o)$, so the $H_a$ complicates matters somewhat.

Let me show you how the $H_i$ is obtained from $H_a$, where you really need a $B_a$ with a subscript for the applied $B$, where $B_a=\mu_o H_a$.
$E_i=E_a-P/(3 \epsilon_o)$ using the demagnetizing factor $D=1/3$ for a sphere.
Now $P= P_i=\epsilon_o \chi E_i$ so $E_i=E_a/(1+\frac{\chi}{3})$, so that $H_i=H_a/(1-\frac{|\chi|}{3})$, and $M=-\mu_o |\chi| H_i=-|\chi|B_a/(1-\frac{|\chi|}{3})$, and $B_i=\mu_o(1+\chi )H_i=B_a(1-|\chi|)/(1-\frac{|\chi|}{3})$.

Note: $M=\mu_o \sigma R \omega$, but not every formula works for that solution, because of the $B_a$.

Once we get agreement with the inside, then we'll take a closer look at the outside. Please let me know if you were able to follow the calculations.

Yes I was able to follow the calculations.
Would B_outside be $$-\frac{M_0 R^3}{3 \mu_0 r^2} \left( \cos(\theta) \mathbf{\hat{r}} + \frac{\sin(\theta)}{r}\mathbf{\hat{\theta}} \right)$$?

 

[Charles Link]

Would B_outside be

See the last link of post 5. It's post 7 of the "link". I would need to study this in detail=I don't have extra time at the moment, but don't forget to include $B_a$ besides the contribution to $B$ from the magnetization. For the magnetization, you of course need to use what I just computed in post 8.

 

[Charles Link]

and a follow-on: For the $\hat{a}_r$ component, when you take the derivative of $1/r^2$, you get $-2/r^3$, (using the gradient per the link I mentioned above). I'm not going to check all of the signs, but what you have looks almost correct, but both terms are with a $1/r^3$. Don't forget to include the original $B_a$ though.

 

[milkism]

and a follow-on: For the $\hat{a}_r$ component, when you take the derivative of $1/r^2$, you get $-2/r^3$, (using the gradient per the link I mentioned above). I'm not going to check all of the signs, but what you have looks almost correct, but both terms are with a $1/r^3$. Don't forget to include the original $B_a$ though.

True, also forgot to take the negative when doing the gradient it should be this $\frac{M_0 R^3}{3 \mu_0 r^3} \left( 2\cos(\theta) \mathbf{\hat{r} + \sin(\theta)}\mathbf{\hat{\theta}} \right)$. So we have $B_i = B_a - \frac{M}{3 \mu_0}$

 

[Charles Link]

Looks good for $B_{outside}$, but add $B_a=B_o \hat{z}$.

For $B_i$, what I have in post 8 is complete. (You don't need to add any $B_a$ to that). The expression $B_i=B_a-M/(3 \mu_o)$ is not correct though=we have $H_i =H_a-M/(3 \mu_o)$, but $B_i=\mu_o H+M=\mu_o H_a-M/3+M=B_a+(2/3)M$.

 

[Charles Link]

One additional item=I put the "link" in post 5 above, but I think this one is worth repeating=this "link" ties together the magnetic surface current method and the magnetic pole method with a simple example. You should find it good reading. See https://www.physicsforums.com/threads/a-magnetostatics-problem-of-interest-2.971045/
It should be noted that currents in conductors also contribute to $H$ in the pole method, with a calculation using Biot-Savart divided by $\mu_o$. I may have mentioned this later in the thread, but I don't see it in the first couple of posts.