A line integral about a closed "unit triangle" around the origin

[brotherbobby]

Homework Statement

Show that $\boxed{\oint_C x^2 y \mathrm{d} s = -\frac{\sqrt{2}}{12}}$ where $C$ is the closed triangle shown in the figure below.

Relevant Equations

This is an example of a "line integral" of the form $\int_C \psi(x,y,z) ds$. (I am not sure what relevant equations to add here. I'd prefer to get right into my attempt of this question).

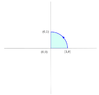
Problem statement : As a part of the problem, the diagram shows the contour $C$above on the left. The contour $C$ is divided into three parts, $C_1, C_2, C_3$ which make up the sides of the right triangle.

Required to prove : $\boxed{\oint_C x^2 y \mathrm{d} s = -\frac{\sqrt{2}}{12}}$.

Attempt : We note straightaway that the line integral must be zero on lines $C_1, C_3$ as the values of $x,y$ are zero on $C_1$ and $C_3$ respectively. I require to find the line integral on the line $C_2$.

The integral $$I = \int_{(1,0)}^{(0,1)} x^2y\, \mathrm{d}s$$ The line itself has the equation : $x+y=1\Rightarrow y=1-x$. From the diagram above, $s$ and $x$ are oppositely directed along the line $C_2$. Hence we have $ds=-\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx$. The derivative $dy/dx = -1\Rightarrow ds = -\sqrt{2} dx$.

Writing the integral I entirely in terms of $x$, we get : $$\small{I = \int_{(1,0)}^{(0,1)} x^2y\, \mathrm{d}s = \int_1^0 -x^2(1-x)\sqrt{2} dx=\sqrt{2}\int_0^1 (x^2-x^3) dx= \sqrt{2} \left| \frac{x^3}{3} - \frac{x^4}{4}\right|_0^1= \sqrt{2}\left(\frac{1}{3}-\frac{1}{4}\right)=\boxed{\frac{\sqrt{2}}{12}}}$$

My answer is incorrect by the opposite sign. I must confess that I fail to see where I went wrong. Both variables $x,y$ are positive in the first quadrant where the integral is carried out. The contour $C$ is traversed in a counter-clockwise manner, which is positive by the right-hand screw rule. Still, any hint or help would be welcome.
I have a second matter regarding this problem. How can it be done using (plane) polar coordinates? I can write both $x=\rho \cos\phi$ and $y=\rho\sin\phi$ in polar coordinates, but I am confused as to how to write the line element $\mathrm{d}s$ in polar form. Still, any hint or help would be welcome.

 

[Orodruin]

Homework Statement:: Show that $\boxed{\oint_C x^2 y \mathrm{d} s = -\frac{\sqrt{2}}{12}}$ where $C$ is the closed triangle shown in the figure below.
Relevant Equations:: This is an example of a "line integral" of the form $\int_C \psi(x,y,z) ds$. (I am not sure what relevant equations to add here. I'd prefer to get right into my attempt of this question).

My answer is incorrect by the opposite sign. I must confess that I fail to see where I went wrong. Both variables x,y are positive in the first quadrant where the integral is carried out. The contour C is traversed in a counter-clockwise manner, which is positive by the right-hand screw rule. Still, any hint or help would be welcome.

The result is obviously positive as all entities in the integral are non-negative and ds as a differential is also positive. This is regardless of the contour direction.

 

[brotherbobby]

The result is obviously positive as all entities in the integral are non-negative and ds as a differential is also positive. This is regardless of the contour direction.

Thank you @Orodruin. I didn't realize that the contour direction is unnecessary. However, it raises quite a simple doubt in my mind. Let me draw a picture for you just to make it clearer.

The function $y=\sqrt{1-x^2}$ is integrated anti-clockwise from $x=1$ to $x=0$ as shown above. The result is the area of the quadrant, shaded in light blue. If you do the integral, it comes out to be $-\frac{\pi}{4}$. Yet, according to your reasoning above, all entities in the integral are non-negative and the arc element $\mathrm{d}s$ is by definition non-negative. What explains the negative answer then?

[This is all the more baffling for me since the element is traversed in a counter-clockwise sense, which I had always imagined as giving a positive answer, according to the right hand cork-screw rule!]

 

[Orodruin]

The function y=1−x2 is integrated anti-clockwise from x=1 to x=0 as shown above. The result is the area of the quadrant, shaded in light blue.

Please write down the integral you are referring to.

 

[brotherbobby]

Please write down the integral you are referring to.

The integral is $$\int_{x=1}^{x=0} \sqrt{1-x^2} dx\;\;\text{(anti-clockwise).}$$ There is no $ds$ here; nonetheless, all entities are non-negative and so should be the result of the integration.

However, the answer turns out to be $-\pi/4$.

 

[Orodruin]

There is no ds here; nonetheless, all entities are non-negative and so should be the result of the integration.

No, dx is negative in your integral. It is also not a particular curve integral.

 

[brotherbobby]

No, dx is negative in your integral. It is also not a particular curve integral.

Thank you. Sorry for the oversight.

However, what did you mean by "it is not a particular curve integral"? It is a function $y=f(x)$ integrated with respect to $x$, the function can be plotted as a curve. Did you mean it's not a line integral, i.e. an integration along a curve?

I would like to return to my current example of $\int_1^0 \sqrt{1-x^2}dx$ (see my picture above). I agree that the integral should be negative because dx is negative. However, the integral yields the area that the curve makes with the x-axis. If we don't consider how a region of area was traversed, clockwise or anticlockwise, why should its sign come into the picture? Shouldn't all areas be positive irrespective whether the integrating variable or the integrand was positive or negative?

 

[brotherbobby]

Hi all. I want to return to my problem above in my attempt to do it using (plane) polar coordinates. I have made some progress but could not complete. Let me state the problem to begin with.

Problem statement : Show that $\boxed{\int_C x^2y ds = \frac{\sqrt{2}}{12}}$ where C is the contour of the closed triangle shown in the figure above.Attempt : The integral is 0 for both along the x and y-axis lines, marked as $C_1$ and $C_2$, since the values of variables $y$ and $x$ are 0 respectively on those curves. The line on which to carry out the integral is given by $C_2$.

I do the calculation using Autodesk's Sketchbook $^{\circledR}$ software. I hope I am not in violation of anything.

Sorry for the small writing above. Any hint with the integral $$I=\sqrt{2} \int_0^{\pi/2} \frac{\cos^2\phi \sin\phi}{(\sin\phi+\cos\phi)^5}d\phi,$$
would be welcome.

 

[Infrared]

There very well may be a faster way, but the half angle substitution $t=\tan(\phi/2)$ will turn your integrand into a rational function. See https://en.wikipedia.org/wiki/Weierstrass_substitution

Is there a reason you want to do this integral in polar coordinates?

 

[brotherbobby]

Thank you @Infrared for your help. I haven't tried it yet, but more to the point - my final expression up there is mistaken. I am supposed to get the answer $\sqrt{2}/12\approx 0.12$. Instead the expression above, $$I=\sqrt{2} \int_0^{\pi/2} \frac{\cos^2\phi \sin\phi}{(\sin\phi+\cos\phi)^5}d\phi \approx 0.081,$$ which is significantly different.

I would like to ask you to go through my calculations and reasoning up there, when you have the time, and tell me where am mistaken.

Is there a reason you want to do this integral in polar coordinates?

Well, just for confidence's sake. I have solved the given integral by writing it out entirely in the $x$ and then in the $y$ variables. My original post #1 actually has the details for the integral written out in the $x$ variable. However, long ago my teacher told me that all (line or surface) integrals must be possible via a change of coordinates. It restores faith, if you will understand, when you can solve the same problem in a different way.

My workings up there in post #8 are too small for the eye. Please click on it and zoom (CTRL & +) to see if it helps. I am willing to re-do the mathematics on here using PF's latex-like format if you request.

 

[vela]

Thank you @Infrared for your help. I haven't tried it yet, but more to the point - my final expression up there is mistaken. I am supposed to get the answer $\sqrt{2}/12\approx 0.12$. Instead the expression above, $$I=\sqrt{2} \int_0^{\pi/2} \frac{\cos^2\phi \sin\phi}{(\sin\phi+\cos\phi)^5}d\phi \approx 0.081,$$ which is significantly different.

You must have evaluated the integral incorrectly. When I plugged it into Mathematica, I got the expected result.

 

[brotherbobby]

You must have evaluated the integral incorrectly. When I plugged it into Mathematica, I got the expected result.

Thank you @vela . I forgot to put the $\sqrt 2$ before the integral before when I calculated it.

Now, all that is good using the internet calculators or softwares like Mathematica. How do I do the integral analytically - $$I=\sqrt{2} \int_0^{\pi/2} \frac{\cos^2\phi \sin\phi}{(\sin\phi+\cos\phi)^5}d\phi\;\;?$$

I have tried and failed with the substitution $t = \tan\phi/2$. A hint would be very welcome.

 

[brotherbobby]

I have succeeded in carrying out the above integral, sorry to bother you all. I put the details below.

We have $$I=\sqrt{2} \int_0^{\pi/2} \frac{\cos^2\phi \sin\phi}{(\sin\phi+\cos\phi)^5}d\phi.$$ Let us put $\tan\phi=z\Rightarrow \sec^2\phi d\phi = dz$ and our integral becomes $$I = \sqrt 2\int_0^{\infty} \frac{zdz}{(1+z)^5}.$$ Let us change variables again making $1+z=y\Rightarrow z= 1-y\Rightarrow dz = dy$. Our integral $$I = \sqrt 2 \int_1^{\infty} \frac{y-1}{y^5}\; dy = \sqrt{2} \int_1^{\infty} (y^{-4}-y^{-5})dy=\sqrt{2} \left[ \frac{y^{-4}}{4} - \frac{y^{-3}}{3} \right]_1^{\infty} = \sqrt{2}\left(\frac{1}{3}-\frac{1}{4}\right)=\pmb{\frac{\sqrt{2}}{12}}$$