A little clique "game" in Java - Clique Problem

[Jeronimus]

For what it's worth, i created a little java program in relation to the clique problem

https://en.wikipedia.org/wiki/Clique_problem

The idea was, to play around with it and maybe discover some better algorithm than the known ones used to discover all maximum cliques

The code is quite small and can be found here

http://pastebin.com/zUuEscqu

You have to compile it yourself using javac (should work both in linux and windows but i have tested only windows)

An easier method for those who do not know much about programming, would be to download the free drjava IDE (google it) and just copy and paste the code into the IDE. Then hit the compile button and the run button after.
Make sure you have Java installed on your system however.

Here is an image of how this would look like, with the program running on the top left side and the drjava IDE with the code pasted into it.

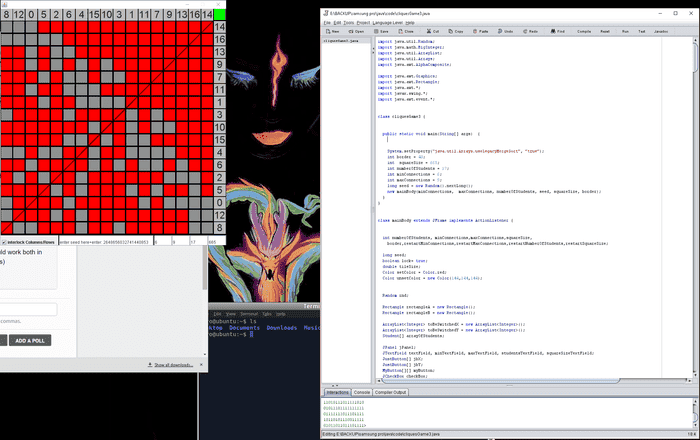
From left to right, the boxes you can enter numbers into act as follows:

1) You can enter a seed for the random number generator or have the program generate one randomly for you.
2) The minimum connections a student or node will build to another student or node.
(The program generates connections for a particular node to other nodes. A minimum of 6 connections will be generated with default values for a particular node.
However, other nodes might also generate connections to this node as they are generated, so the number of connections to other nodes will be greater than this value most likely.)

3) The maximum connections
4) The number of students/nodes
5) The size of the program box in pixels. Increase the number if you have a larger monitor

The green button top right will generate a binary output of the small squares (0 = grey square 1 = red square) in the command line or drjava interaction pane.

The idea is to find the most efficient way of generating a square made up of red squares like the one top right. Red squares symbolize the nodes being connected or "the students know each other, hence are part of a clique".
In this case 1,11,7,9,13,16,14 are part of a clique.

As long as the checkbox bottom left of the program is checked, the columns and rows remain at the same position as you move them.
But you can remove this lock if you believe that it would help you discover an algorithm easier that way.
You just have to make sure that the numbers in the columns and row next to the large square, made out of smaller red squares, are the same. Hence whatever numbers are in the column section of the red square, are also in the row section.

example:

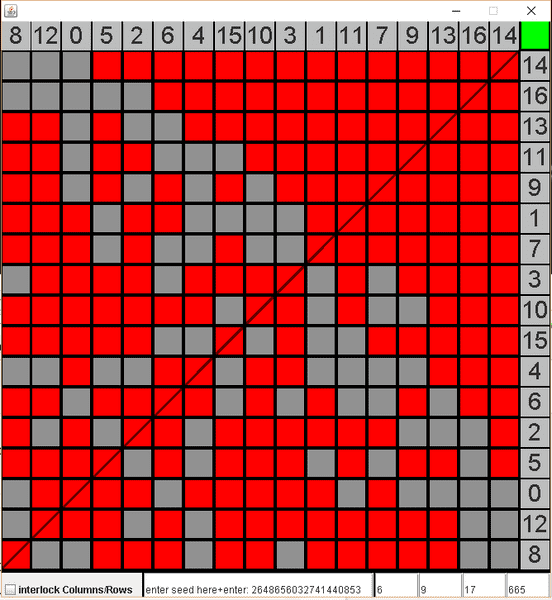
Here i removed the lock bottom left. The order of the numbers in the row section of the large square, made up of smaller red squares, does not correspond to the order of the column section any more. It is the same clique still however. 1,7,9,11,13,14,16 being part of one clique.

Hope some might find this little code interesting. Feel free to use the code in any way you like as long as you do not try to prevent others from using it in any way they like :)

 

[Greg Bernhardt]

Looks good, nice work!

 

[Jeronimus]

Looks good, nice work!

Thanks. However, more accurate would have been "Looks good, it works". I am just a hobby programmer, not coding much really and i made a terrible mistake in this code. It only works because of "luck" in a sense.

I used if (str==("<some String>")){ to compare the strings but the proper way is if (str.equals("<some String")){

The only reason it worked, is because the JVM is smart enough to use the same reference for equal strings. But that isn't always the case, so it might break for other programs.
So i was comparing the references rather than the strings themselves.

Here is the fixed version http://pastebin.com/zpReBGK0
also cleaned of some obsolete System.out.println calls i used for debugging and forgot to remove.

It's not really absolutely necessary to use the new version. The old works i guess because i got lucky, but i had to set this straight for anyone who actually wants to use part of the code for their own projects.