A massless disk with an embedded particle rolls down an inclined plane

[annamal]

Homework Statement

A massless disk of radius R has an embedded particle
of mass m at a distance R/2 from the center. The disk is released from rest in the position
shown below and rolls without slipping down the fixed inclined plane. Find the velocity

Relevant Equations

v = dr/dt

This is the problem:

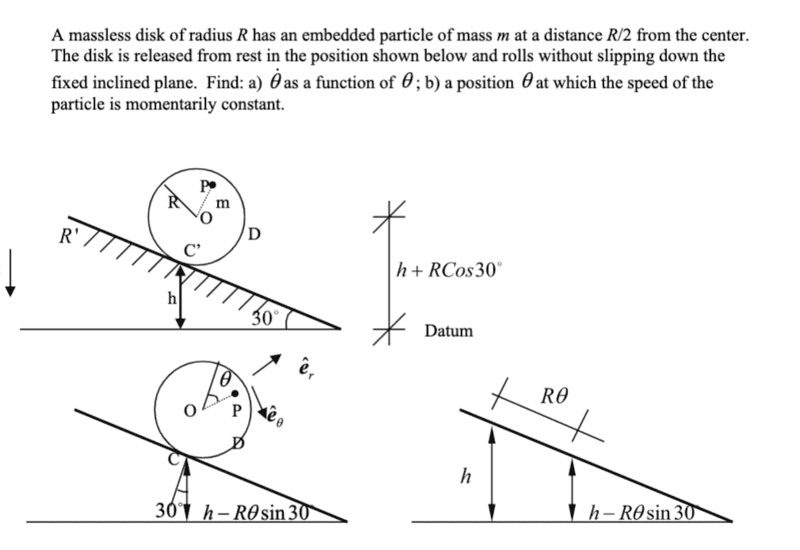
I am a little confused at the solution below. Since $\vec r_{P/C} = (R/2)*(5 + 4cos(\theta))^{0.5}\ \vec e_r$, I am wondering why there is no vector e_r component for the velocity. I know that d(R)/dt = 0, but you can still get a derivative in the $\vec e_r$ direction from dcos(theta)/dt

 

[haruspex]

The solution is unclear to me. In the ground frame, $\dot{\hat e_r}$ is nonzero, but ${\hat e_r}$ is treated as a constant.
Much easier to note that using $\hat i$ parallel to the slope, etc., the velocity of O is $R\dot\theta\hat i$ and relative to that the velocity of P is $\frac 12R\dot\theta(\cos(\theta)\hat i-\sin(\theta)\hat j)$. Add those and sum the squares of the orthogonal components.

 

[TSny]

The unit vectors $\hat e_r$ and $\hat e_{\theta}$ are not drawn very accurately in the figure here:

$\hat e_r$ should be in the direction of $\vec r^{P/C}$ as shown here:

[EDIT: I'm not sure about the unit vector $\hat e_{\theta}$. I drew it as being perpendicular to $\hat e_r$. But, maybe $\hat e_{\theta}$ is defined to be perpendicular to line OP. If so, then $\hat e_{\theta}$ is not perpendicular to $\hat e_r$. Oh, wait. In the solutions it states $\hat k = \hat e_r \times \hat e_{\theta}$, so these three unit vectors are mutually perpendicular, and the direction of $\vec v^{P/C}$ is $\hat e_{\theta}$.]

In the ground frame, $\dot{\hat e_r}$ is nonzero, but ${\hat e_r}$ is treated as a constant.

I don't think they treated $\hat e_r$ as a constant. They didn't find $\dot {\vec r}^{P/C}$ by taking the time derivative of $\vec r^{P/C}$.

They used the fact that the velocity of $P$ relative to the lab is the same as the velocity of P relative to the instantaneous center of rotation of the disk (at C). Thus, $\dot {\vec r}^{P/C} = \vec{\omega}^{\rm disk} \times \vec r^{P/C}$, where $\vec{\omega}^{\rm disk} = \dot {\theta} \hat k$.

 

[haruspex]

The unit vectors $\hat e_r$ and $\hat e_{\theta}$ are not drawn very accurately in the figure here:
View attachment 341760

$\hat e_r$ should be in the direction of $\vec r^{P/C}$ as shown here:
View attachment 341761



I don't think they treated $\hat e_r$ as a constant. They didn't find $\dot {\vec r}^{P/C}$ by taking the time derivative of $\vec r^{P/C}$.

They used the fact that the velocity of $P$ relative to the lab is the same as the velocity of P relative to the instantaneous center of rotation of the disk (at C). Thus, $\dot {\vec r}^{P/C} = \vec{\omega}^{\rm disk} \times \vec r^{P/C}$, where $\vec{\omega}^{\rm disk} = \dot {\theta} \hat k$.

Ok.
Do you know what that LHS superscript notation means?
$^{R^?}v^{P/C}$
It is too blurry to read the "?".

 

[TSny]

Do you know what that LHS superscript notation means?
$^{R^?}v^{P/C}$
It is too blurry to read the "?".

It looks like $R'$. This notation $R'$ appears in the first figure near the top of the ramp. Maybe it's something to do with denoting the frame of reference. Thus, $^{R\,'} \vec v^{P/C}$ is the velocity of P relative to C in the frame $R'$ as opposed to the frame of the rotating disk. I'm not sure.

 

[annamal]

It looks like $R'$. This notation $R'$ appears in the first figure near the top of the ramp. Maybe it's something to do with denoting the frame of reference. Thus, $^{R\,'} \vec v^{P/C}$ is the velocity of P relative to C in the frame $R'$ as opposed to the frame of the rotating disk. I'm not sure.

Yes it is $^{R\,'} \vec v^{P/C}$

 

[annamal]

It looks like $R'$. This notation $R'$ appears in the first figure near the top of the ramp. Maybe it's something to do with denoting the frame of reference. Thus, $^{R\,'} \vec v^{P/C}$ is the velocity of P relative to C in the frame $R'$ as opposed to the frame of the rotating disk. I'm not sure.

It is $^{R\,'} \vec v^{P/C}$ and means the reference frame of R' which is the reference frame of the slope and disk.

 

[annamal]

Ok.
Do you know what that LHS superscript notation means?
$^{R^?}v^{P/C}$
It is too blurry to read the "?".

It is $^{R\,'} \vec v^{P/C}$ and means the reference frame of R' which is the reference frame of the slope and disk.

 

[haruspex]

am wondering why there is no vector e_r component for the velocity

As @TSny wrote, $\hat e_r$ is always along the line CP, and $\hat e_\theta$ is always normal to that. Since C is the instantaneous centre of rotation, there is no velocity component along CP.

 

[annamal]

As @TSny wrote, $\hat e_r$ is always along the line CP, and $\hat e_\theta$ is always normal to that. Since C is the instantaneous centre of rotation, there is no velocity component along CP.

ok but how do you explain this mathematically? I thought $\frac{d\vec r}{dt} = \vec v^{P/C}$.
Since $\vec r^{P/C} = (R/2)*(5 + 4 cos\theta)^{1/2} \vec e_r$,
the derivative of that is
$(R/4)*(5 + 4cos\theta)(-4sin\theta)^{-1/2}\dot{\theta} \vec e_r + ...\vec e_{\theta}$. Mathematically like that, the only way to have no $\vec e_r$ is for $\dot{\theta} = 0$

 

[haruspex]

ok but how do you explain this mathematically? I thought $\frac{d\vec r}{dt} = \vec v^{P/C}$.
Since $\vec r^{P/C} = (R/2)*(5 + 4 cos\theta)^{1/2} \vec e_r$,
the derivative of that is
$(R/4)*(5 + 4cos\theta)(-4sin\theta)^{-1/2}\dot{\theta} \vec e_r + ...\vec e_{\theta}$. Mathematically like that, the only way to have no $\vec e_r$ is for $\dot{\theta} = 0$

The confusion arises from the definition of C.
For the logic used in the text, and as described by @TSny , C is a point fixed on the ramp where contact is made at some instant. With that definition, the equation for $\vec r^{P/C}$ does not remain true over time.
If we change it to be defined as the point of contact at each instant then the equation can be validly differentiated, but then the derivative does have an $\vec e_r$ term.

 

[PeroK]

Note that kinetic energy is invariant under rotation of the system. The kinetic energy as a function of theta, therefore, is the same as for the mass rolling along a flat surface. Taking the origin at the centre of the mass we have:
$$x = R\theta + \frac R 2 \sin \theta, \ y = \frac R 2 \cos \theta$$$$\dot x = R\dot \theta(1 + \frac 1 2 \cos \theta), \ \dot y = -\frac 1 2 R\dot \theta \sin \theta$$$$T = \frac 1 2 m(\dot x^2 + \dot y^2) = \frac 1 2 mR^2\dot \theta^2\big(\frac 5 4 + \cos \theta \big )$$$$= \frac {mR^2}{8}\big(5 + 4\cos \theta \big )\dot \theta^2$$

 

[Lnewqban]

Note that kinetic energy is invariant under rotation of the system. The kinetic energy as a function of theta, therefore, is the same as for the mass rolling along a flat surface.

Could you explain that a little further?
I am probably confused, but I visualize a cycloid trajectory (respect to the sloped surface) of the embedded particle P of mass m.

Induced solely by gravity acting on that mass, I see the rotational velocity of the disk as not constant but increasing while reaching a point prior to C (vertical line with the center of the disk) and decreasing while moving away from that point of minimum potential energy respect to C.

 

[PeroK]

Could you explain that a little further?

Clearly the function $T(\theta, \dot \theta)$ is independent of the angle of the slope.

 

[haruspex]

Clearly the function $T(\theta, \dot \theta)$ is independent of the angle of the slope.

Yes, better would have been "theta and its time derivatives".

 

[PeroK]

Yes, better would have been "theta and its time derivatives".

I must have been in a Lagrangian mood.

 

[annamal]

They used the fact that the velocity of $P$ relative to the lab is the same as the velocity of P relative to the instantaneous center of rotation of the disk (at C). Thus, $\dot {\vec r}^{P/C} = \vec{\omega}^{\rm disk} \times \vec r^{P/C}$, where $\vec{\omega}^{\rm disk} = \dot {\theta} \hat k$.

What is this "lab" you are referring to?

 

[haruspex]

What is this "lab" you are referring to?

@TSny means the "lab frame". Also known as the ground frame.